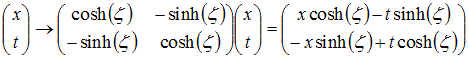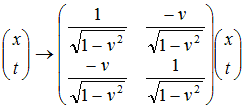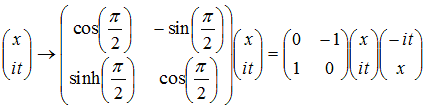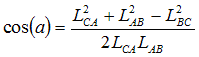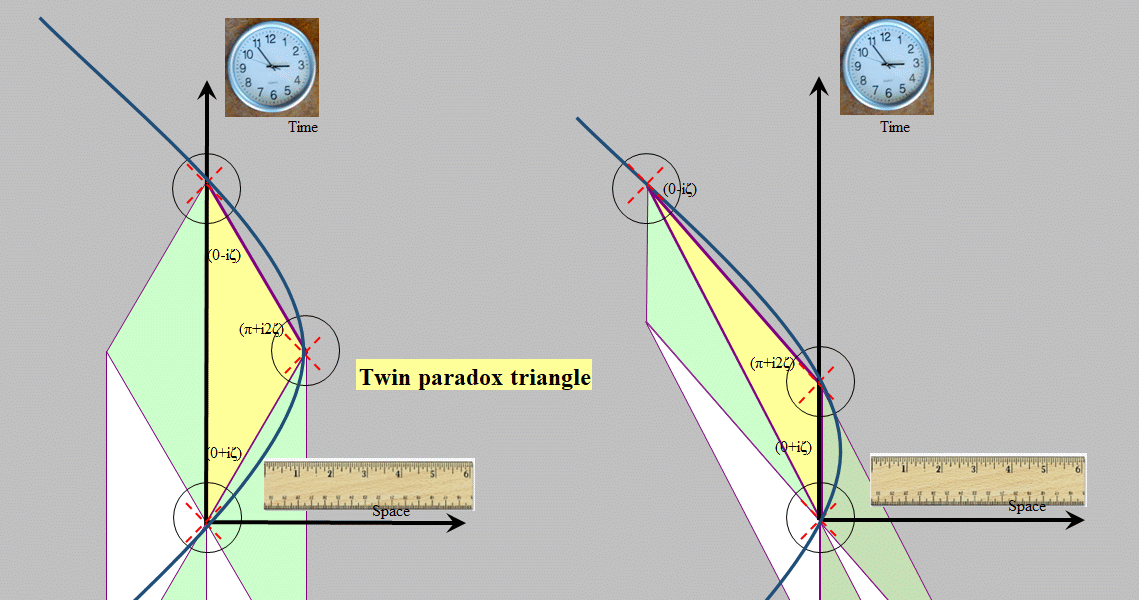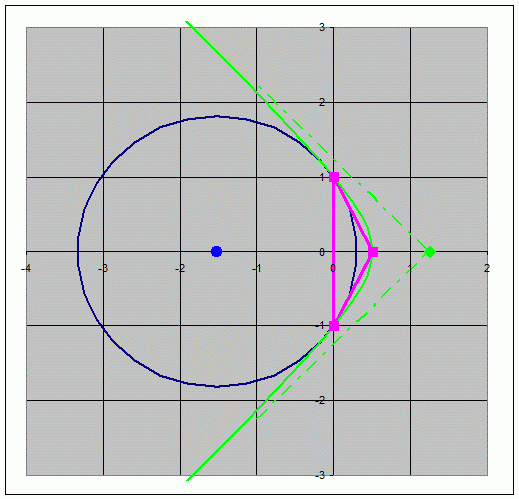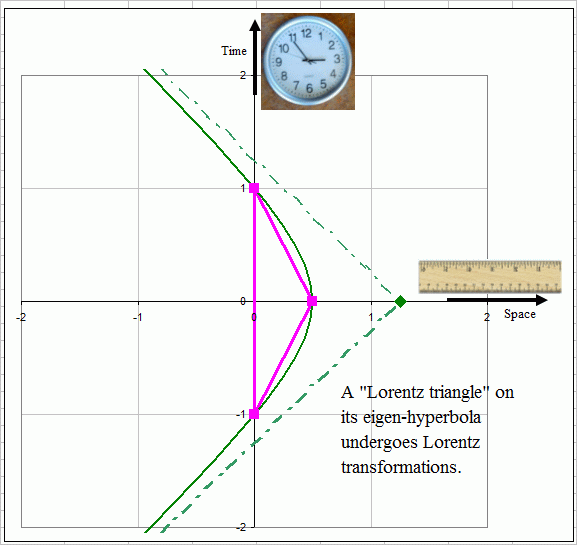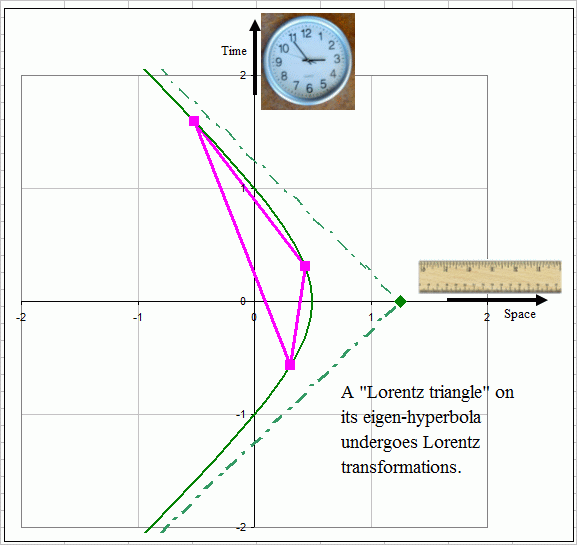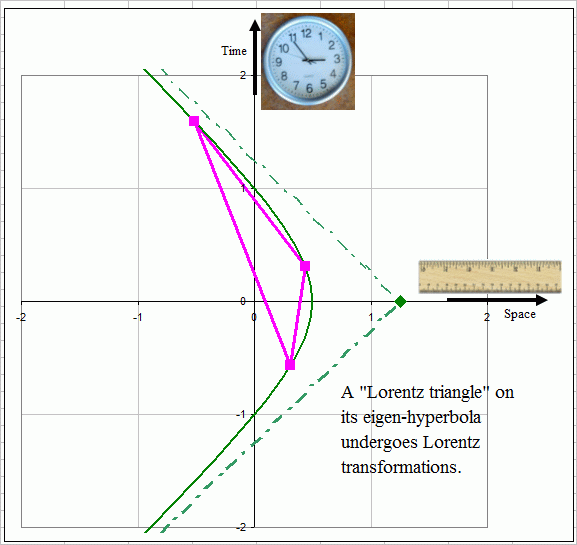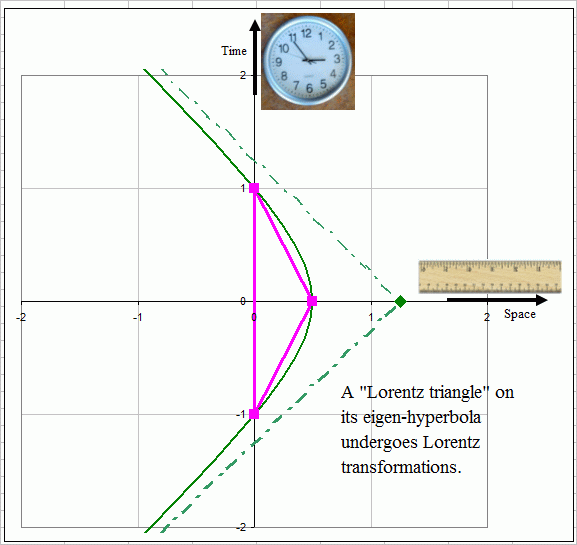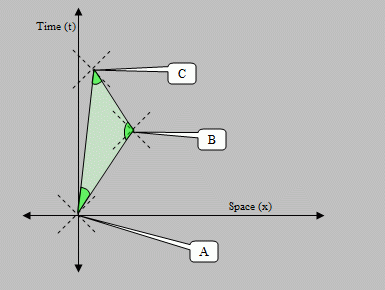
Figure 1: A
triangle in space-time. The 3 dotted crosses represent light cones
emitted from
the 3 vertices. Note that at vertex B, the triangle crosses a light
cone
twice.
Lengths.
In classical physics, lengths are invariant under translation, rotations, and changes in velocity. But in relativistic physics, the “length” that stays invariant under changes in velocity is given by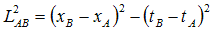
(taking the
speed
of
light c=1
for convenience)
Or, if we think of time as an imaginary-valued space coordinate:
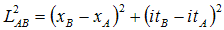
Note:
We should not confuse space-time lengths with coordinates. Coordinates
change with Lorentz transformations, but lengths and time intervals
(sometimes calles eigen-time or proper time) of
a given world line are Lorentz invariant. They are physically
either a time
difference, measured by a clock ,
or a distance, measured by a ruler
,
or a distance, measured by a ruler .
.
Time intervals have negative squared length, or imaginary length, space distances are real valued.
Rotations and Lorentz transformations.
The space-time analogue of rotations are Lorentz transformations.
A rotation in ordinary space can be written as:
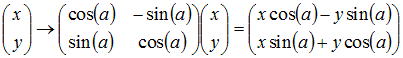
To get Lorentz transformations, simply replace the the y
coordinate by
it, and the angle a by iζ:
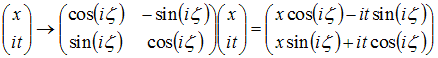
The parameter ζ is called rapidity. It is
essentially
a
relativistically corrected velocity, as shown in the graph below:
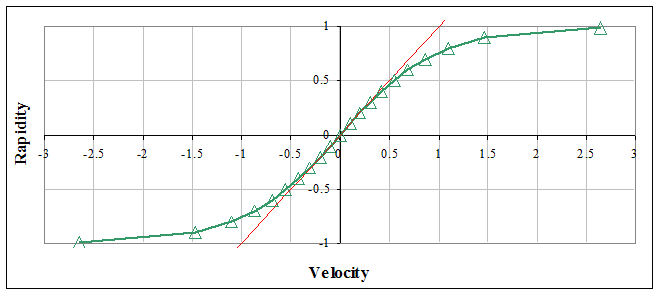
Figure 2: The rapidity(ζ) is a relativistically corrected velocity(v), tanh(ζ)=v
In classical physics, lengths are invariant under translation, rotations, and changes in velocity. But in relativistic physics, the “length” that stays invariant under changes in velocity is given by
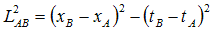
Or, if we think of time as an imaginary-valued space coordinate:
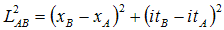
 ,
or a distance, measured by a ruler
,
or a distance, measured by a ruler .
.Time intervals have negative squared length, or imaginary length, space distances are real valued.
Rotations and Lorentz transformations.
The space-time analogue of rotations are Lorentz transformations.
A rotation in ordinary space can be written as:
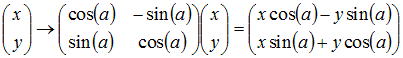
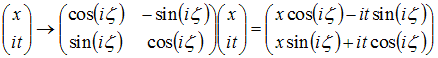

Figure 2: The rapidity(ζ) is a relativistically corrected velocity(v), tanh(ζ)=v
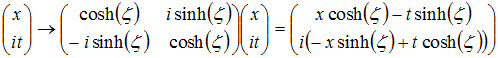 (eq2)
(eq2)