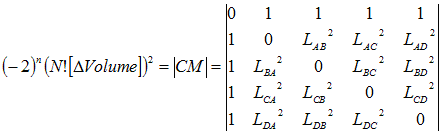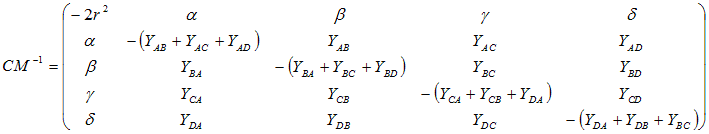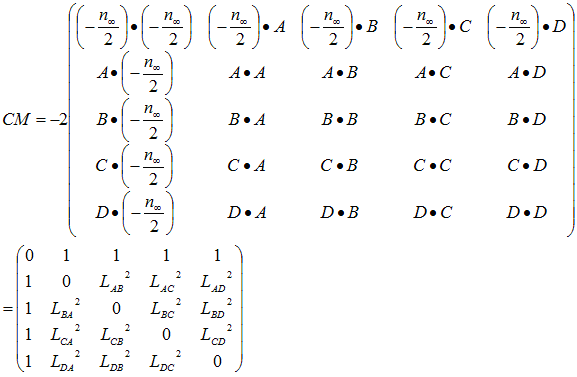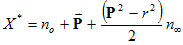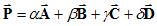A formula for the N-circumsphere of an N-simplex .

My website is  moving.  Best go to the  new location at westy31.nl/Circumsphere/ncircumsphere.html      This old page will be gone soon...

G.Westendorp

april 2013

Note: For a much shorter proof skip to here. (I don't want to delete the long proof just yet)

We show that the circumradius and circumcentre of the N-circumsphere of an N-simplex are obtained directly from elements of the inverse (CM^-1) of the Cayley Menger matrix (CM ) for the N-simplex.

In 3 dimensions, if:

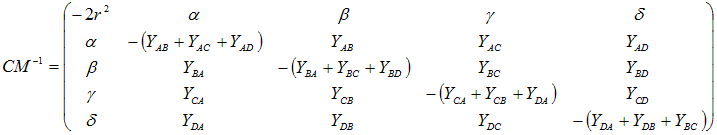
Then (α, β, γ, δ) are the 4 barycentric coordinates of the circumcentre and r is the circumradius. This generalises to N-dimensions in a straightforward manner.

Our formula provides a compact expression for the circumcentre and circumradius that it is coordinate independent in the sense that it requires only the squared distances between the vertices. We will use the conformal model of geometric algebra for the proof, but the equation itself uses only the Cayley-Menger matrix.

An N-circumsphere is an N-dimensional sphere, that passes through the (N+1) points of an N-simplex. In 2 dimensions, it is most easily visualised and corresponds to the circumcircle.

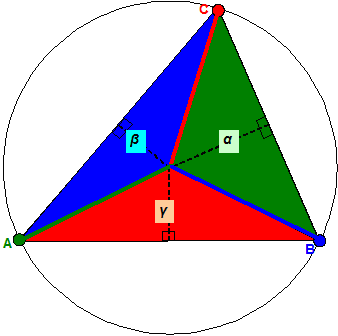
The circumcircle of a triangle, with the barycentric coordinates (α, β, γ) of the circumcentre shown as areas of 3 subtriangles, opposite to the vertices (A,B,C) respectively.

For any N-simplex, we can write down the Cayley-Menger matrix, best known for the Cayley-Menger determinant, which is used to compute the N-volume of the N-simplex in terms of the squared distances between the vertices. We write it in N=3 dimensions (ie for a tetrahedron), assuming the generalisation to N-dimensions to be obvious:

The required parameters for the circumsphere are obtained directly from the inverse of CM. If this inverse CM^-1 is written as:

Eq 1

Then (α, β, γ, δ) are the 4 barycentric coordinates of the circumcentre and r is the circumradius. If required, we can convert the barycentric coordinates (α, β, γ, δ) to the Euclidean coordinates of the circumcentre (x,y,z):

(x,y,z)= α(xA,yA,zA) + β(xB,yB,zB) + γ (xC,yC,zC) + δ (xD,yD,zD)

Eq 2

To prove this, we will use the machinery of conformal geometric algebra. We refer to [1] for an explanation of the terminology and principles of conformal geometric algebra. An important reason it is useful for our problem, is that the internal product of 2 points in the conformal model is equal to -1/2 times the squared distance between the corresponding Euclidean points. Using this fact we can see that the Cayley-Menger matrix is -2 times to the Grammian matrix of the 4 points (A,B,C,D) of the tetrahedron, together with minus half the ‘point at infinity’ (-n_∞/2):

Eq 3

Next, we use another nice feature of conformal geometric algebra, that a sphere (X) through points (A,B,C,D) is given by the exterior product of these points:

X=A^B^C^D

(ie. the sphere is the set of points (p) that satisfy p ^ X = 0)

The circumcentre and circumradius can be found by computing the Hodge dual of X* of X. The Hodge dual of a sphere with radius (r) and centre (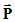) has the form:

Eq 4

So from the Hodge dual, we can read of the centre as the Euclidean part, and then use the (n_∞) component to obtain r²

The computation of X* uses the contraction (_┘) with the pseudoscalar and the expansion of a point P in into its Euclidean part and the extra dimensions (n_o) and (n_∞):

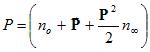
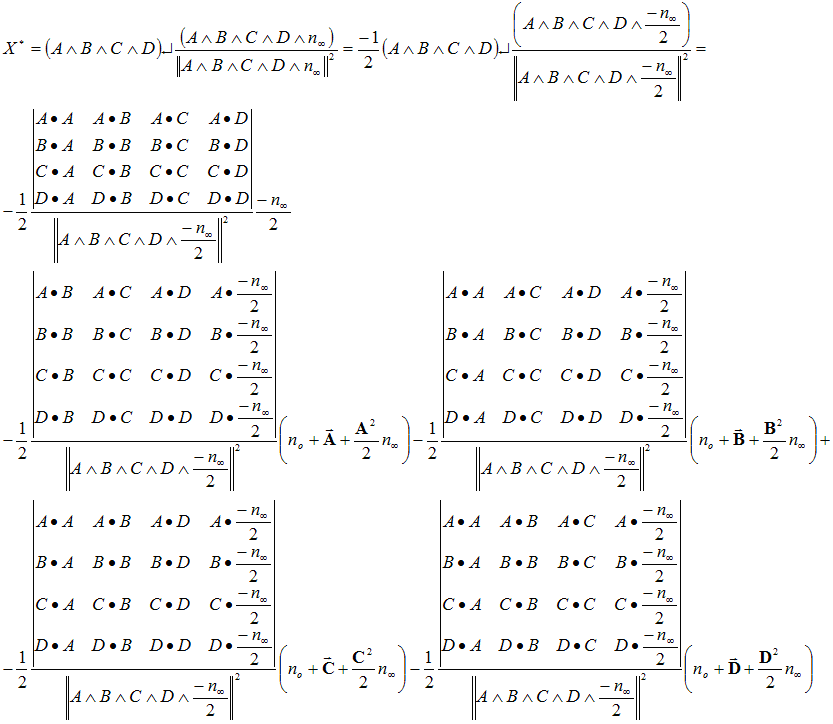
The determinant terms in the above expansion of the X^* correspond to the cofactor expansion for the inverse of top row of CM, so we can replace these determinant terms with the coefficients from Eq 1:

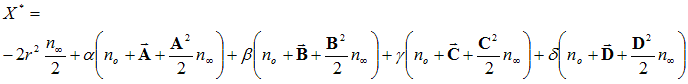
(Eq 5)

Comparing the Euclidean parts of equations 4 and 5, we find the expression for the centre ():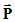

Eq 6

We can verify that the n₀ components of equation 5 add to 1 by noting that:

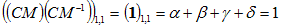
To justify that we labelled element (1,1) of CM^-1 as -2r², we first check that if the circumcentre is at the origin, then the n_∞ component of X^* according to Eq 5:

This is indeed the correct value for the dual a circumsphere at the origin.

(We used .)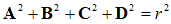

So our expression for CM^-1_(1,1) is valid if the sphere is at the origin. But the elements of the Cayley-Menger matrix are invariant under translations, and so is the circumradius, therefore the element (1,1) must remain equal to -2r².

Finally, we mention an interpretation of the other terms (Y_ij) in equation 1. The original motivation for this work was in fact to find an expression for resistance values in terms of squared lengths for N-simplexes that discretise a conducting medium. As we  discuss in another webpage, Y_ij =1/R_ij , where R_ij is the effective resistance value between vertices i and j of the N-simplex. (Assuming unit specific conductivity of the medium)

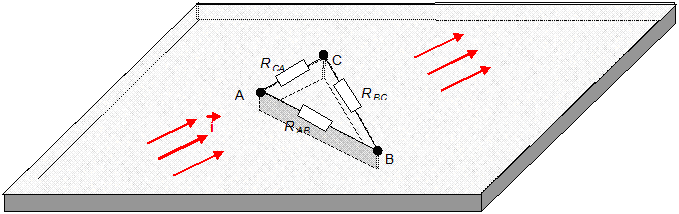
Illustration for the interpretation of Y_ij =1/R_ij as the effective conductance values for simplicial discretisation using electric circuits.

---

Appendix: A proof adapted from a 1930 article by Coxeter.

Max Goering brought a 1930 article by Coxeter [2] to my attention. Coxeter does not actually mention the Cayley menger matrix or its inverse, but from his article I was able to construct the following proof, requiring no conformal geometric algebra. We will show that the N-dimensional sphere containing all (N+1) points of an N-simplex, is found directly from the inverse of the Cayley Menger matrix of the simplex.

In an (N+1) dimensional Euclidean space, let X_i be (N+1) linearly independent vectors. A point (P) may be expressed using Einstein summation convention as:

P = x_iX_i

The X_i also define the vertices of an N-simplex embedded in (N+1)-dimensional space. The condition, Σx_i = 1 defines an N-dimensional subspace, embedded in N+1 dimensions. The x_i are “barycentric coordinates” of this N-dimensional subspace, they are weights such that a coordinate in the N-dimensional space is the weighted sum of the vertices of the N-simplex.

The set of conditions

0 <= x_i <=1

tell us if a point is inside the simplex. This can be very useful!

Let L²_ij be the squared distance between 2 vertices (i and j) of the simplex.

The distance (PQ) between 2 points (P,Q) with barycentric coordinates (p_i and q_j) inside the N simplex is:

-2PQ² = Σ_ij ((p_i-q_i)(p_j-q_j) L²_ij) (eq A1)

So -½L²_ij is a bit the metric tensor for barycentric coordinates, except that barycentric coordinates have one superfluous element.

This is proved by Coxeter, but it may be quickly seen by noting that it is obviously true for any 2 vertices themselves. (The factor 2 arises because the distance occurs twice in the symmetric sum) But the squared length must be linear in the coefficients p_i and q_j, so expression (A1) must be true.

Now let us find the circumsphere, barycentric coordinates (x_i) and radius (R).

The condition may be written:

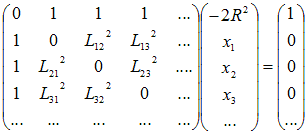
The top line of the matrix multiplication expresses Σx_i = 1. The other lines express the condition, using (A1), that the distance between the circumcentre and a vertex is R².

We recognise the matrix in the above expression as the Cayley Menger matrix (CM), whose determinant is used to compute the N-volume of a simplex.

Now, by using the inverse  CM^-1 we find our result directly:

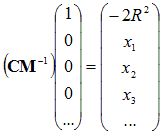
-> CM^-1₁₁ = -2R²

x_j = CM^-1_1(j+1)

References:

1. Dorst, L. et al (2007), Geometric Algebra for Computer Science, Morgan-Kaufmann. ISBN 0-12-374942-5

2. The Circumradius of the General Simplex, H. S. M. Coxeter, The Mathematical Gazette, Vol. 15, No. 210 (Dec., 1930), pp. 229-231