Salvaged GooglePlus Account of Gerard Westendorp - Part1

Move Website
My website is  moving.  Best go to the  new location at westy31.nl/SalvagedGooglePlus/SalvagedGooglePlus_Part1.html      This old page will be gone soon...

In october 2018, it was rumored that Google plus is intending to shut down.
So I salvaged all my posts. 
This is part 1. Here is part 2.
Other stuff by me.
 

Another hinged construction.

This one shows that you could have almost unlimited expansion ratio in ‘auxetic’ materials. I used 3X3 sub-squares, which leads to an expansion factor of 5 for each square but if you go to nxn, the expansion ration becomes (2n-1). (I chopped of the corners of squares that are not a hinge) The red triangles can be shrunk to zero. Now, they actually form an additional degree of freedom, you can hinge them independently. I left them in for aesthetic reasons.

Animated Photo


15 plus ones


A new hinged polyhedron.


Animated Photo


9 comments
Gerard Westendorp:+Alison Grace Martin
Thanks, didn't know some of that. I discoverd various hinged polyhedra years ago, but later I found that Buckminster Fuller had already discovered the octahedral case, which he called the Jitterbug. His first prototype didn't work, he found out as I did that you need to construct hinges that conserve the normal vectors of the faces. One of your references shows a torus tiled by triangles, in a similar way I did the octahedron.
Jon Eckberg:+Gerard Westendorp I think I asked this before but I can't find the exchange. What do you use to render the mechanics?
Gerard Westendorp:+Jon Eckberg I generate '.inc' files for POV-Ray(A freeware raytracer) using VBA. Pov-ray can make a series of .bmp files (the frames). I batch-convert these to .gif, with some cropping and pixel reduction included, using Irfanview, my favorite image viewer. Then make them into an animated gif using the freeware Unfreeze'.
15 plus ones

Cardboard model of Bricard's flexible octahedron

I got sidetracked by the recent discussions by +John Baez and +Greg Egan into making this cardboard model of Bricard's flexible octahedron. The strips represent intersecting faces.

Animated Photo

Comments:
 John Baez: Excellent! From mathematics into physics!
13 plus ones


In case someone wants to make the Bricard flexible ocrtahedron of my previous post, cut out this picture 2 times. The assembly is technically easy, but tricky due to the confusing folds. (glue the strips back to back)

Photo


12 plus ones


Jon Eckberg asked if there is a hexagonal collapsible hinged tiling. Yep! This one is secretly related related to the square case; each hexagon has 4 hinges.

Animated Photo

Comments:
 Jon Eckberg: Boo! That's cheating +Gerard Westendorp ?!
Does a solution exist with hexagonal, (or trigonal) symmetry? A central polygon surrounded by 6 (or 3)?
Gerard Westendorp: +Jon Eckberg Yes, but that one (the hexagon) doesn't collapse all the way, it get just gets smaller by I think a factor 2, as the hexagon overlaps with the triangles. There is also a triangular case, thinking about that still.
Jon Eckberg: +Gerard Westendorp Thanks again for sharing your explorations. I'm enjoying this.
16 plus ones


I don’t think anyone noticed yet that if you continue transforming the hinged tessellation of squares beyond the point that the squares overlap, something surprising happens: At one stage all squares overlap completely, so that you see only a single square.
In fact, if you work out the formula for the translation of square (i,j), for a tessellation in which the squares are rotated by angle alfa and (-alfa) alternating, you get (x,y) = (i,j) * (cos(alfa) + sin(alfa)) So when alfa gets –pi/4, the translations all become zero!

Animated Photo


5 comments
Gerard Westendorp:+Jon Eckberg alfa goes round all the way from 0 to 2pi, and then contininues. You can actually build it, I have a picture somewhere that I will dig up later. Although the mechanical version cannot do full circle, at least mine couldn't.
Gerard Westendorp:
?Found the old photo. I will make a new design, based on laser-cut parts.
Philip Gibbs:
Now it looks like a trimmed chessboard being folded in 4 dimensions.
13 plus ones

Tri-axial weaving the Klein Quartic

+Alison Grace Martin has been doing posts on tri-axial weaving lately. Normally you get a pattern of hexagons surrounded by triangles. But if you replace some of the hexagons by heptagons or pentagons, the fabric gets a elliptic or hyperbolic curvature respectively, as shown in recent posts by Alison. Of course, when I see heptagons, I think of the Klein Quartic, so I suggested weaving it. But I could not resist trying it myself too. I used packing strip instead of bamboo. I had to melt it together a bit using a soldering gun. The resulting fabric has multiple meta-stable shapes. By the way, the strips will automatically form geodesics on the surface they form, since they are by definition on the surface, and are much quite rigid in all directions except in the bending directions. Hmm, that suggests another project, Villarceau_circles… I’ve seen woven tori on the web, but no tri-axial ones. btw2: The closed klein Quartic surface has 21 of these strips as loops. I doubt if you could weave that without severly twisting the strips.

Photo


5 comments
Gerard Westendorp:
+Alison Grace Martin
About the strips being geodecis, in the video below Chaim Goodman Strauss actually uses strips to find geodecis on surfaces.
youtube.com - Math Encounters -- Shaping Surfaces
Gerard Westendorp:+Alison Grace Martin
Aha, that torus looks like it is made up of villarceau circles. Maybe I will get round to a competer model, in which you can vary parametres to see what the result would look like.
Gerard Westendorp:+Gerard Westendorp
But wait, I think Villarceau circles are actually NOT geodesics of the torus. Hmm, better know that beforehand.
13 plus ones

Here is a new version of the deformable Klein Quartic, with assembly instrucitons: https://westy31.nl/ScrapBook/ScrapBook.html#KleinQuartic

Photo


11 plus ones

08-Oct-17
David Eppstein did a post on how to cut an octahedron (or square pyramid= half an octahedron ) so that the cross section is a regular pentagon. I made a cardboard model of this. It would make a cute box, maybe a next project... (Post by David Eppstein: https://plus.google.com/u/0/100003628603413742554/posts/EvRgzZgzEww)

Animated Photo


15 plus ones


Discrete Theorema Egregium

Gauss is quite famous and quite modest, so when he calls something ‘Theorema Egregium’ (remarkable theorem), it might be something worth thinking about. The animation illustrates a discrete version of the theorem: 4 hinged triangles (‘pop-up’) instead of a smooth surface. The ball on the right is its ‘Gauss map’, I explain furtheron.
The area of a spherical polygon is completely determined by its internal angles: It is equal to 2Pi - sum(Pi - angle_i). The nice thing is that you can prove that each (Pi – angle_i) on the gauss map is equal to the apex angle of a pop-up triangle. You can then immediately see the area on the Gauss map stays constant. Observe that each angle on the Gauss map stays constant as the rectangle changes.
The Theorema Egregium is about a curvature called the ‘intrinsic curvature’ or Gaussian curvature, that stays invariant while the extrinsic curvature changes as the surface is folded. If you have a smooth surface in 3D, you can always adjust your local coordinates so that the formula for the surface is locally: z= k1*x^2 + k2*y^2 What Gauss found, is that if you smoothly bend the surface you might change k1 and k2 (defining the extrinsic curvature), perhaps also rotating the principle curvature axes x and y (which always remain orthogonal for smooth surfaces) but the product k1*k2, called the intrinsic curvature always remains constant! Intrinsic curvature may be positive, as in a sphere, zero, as in flat surface or a cylinder, or negative, as in hyperbolic saddle surfaces (see Wikipedia).
A cool thing about Gaussian curvature is that when you integrate it over a surface, you get the ‘total angular deficit’ of the surface. Suppose you discretise the surface, and at each vertex, you add the angles of the polygons meeting there. The deviation from the flat case of 2*Pi is the angular deficit. The sum of all angular deficits is equal to the integral of the Gaussian curvature. For *any* shape that is topologically a sphere, the answer you get is always exactly 4Pi. But if you like watching mathematical Youtube clips, you probably already knew that.
So for the pop-up, we know the analogue of the intrinsic curvature is the angular deficit at the apex. The extrinsic curvatures must be something to do with the folding angles. They are all coupled; as you flatten the pyramid in direction, you sharpen the folds in the other direction. I found a formula for the folding angles (phi1, phi2) related to the angular deficit alfa: " tan(phi1/2)* tan(phi2/2) = sin(alfa/4)" This is valid for 4 equal triangles. There may be a formula valid for arbitrary triangles, but that I have not yet found. This formula is the analogue of k1*k2 = K.
The Gauss map takes a point on a 3D surface, and maps it onto a point on the sphere which has the same normal vector. On our pop-up, we have 4 easily defined normals, the cyan arrows. These can be Gauss-mapped. The folding lines are infinitely sharp, but we can imagine them smoothed out into a set of parallel more subtle folds. These form a geodesic on the Gauss map. So the pop-up is Gauss mapped to a spherical polygon. The area of the spherical polygon always stays constant; it is the total Gaussian curvature. The individual angles on the Gauss map also stay constant! The extrinsic curvatures are related to the arc lengths on the Gauss map.


Animated Photo


10 plus ones

Zero Gaussian curvature Surface

The function in the picture has *zero Gaussian curvature* everywhere, which is why it can be covered by a flat picture of Gauss, without cutting or stretching the picture. Convenient if you want to make it from cardboard: you just print it and glue only the boundary.
According to Gauss ‘theorema egregium’, the thing that remains invariant as you bend (‘develop’) a surface without stretching it is the intrinsic, or Gaussian, curvature. It can be positive, as in a sphere, negative, as in a saddle, or zero, as in a plane or a cylinder, or a cone. My current project is to see if you can deform flat material without infinitely sharp folds into ‘smooth crumples’. I don’t believe that drapes in clothing have either infinite bends or non-zero Gaussian curvature. According to the Nash Kuiper embedding theorem, you *can* actually deform surfaces while keeping the first derivates of the coordinates finite, although not always higher derivatives.
The function Z = x^3-3xy^2, (the real part of the complex function z^3), is called the ‘Monkey Saddle’, because it has 3 depressions instead of 2: 2 for the legs of a monkey, and an extra one for the tail. I was wondering if I could turn this into a function for which the Gaussian curvature is exactly zero everywhere. The reason for following this particular line of thought was actually a bit confused, but I like the answer I got: The function Z = (x^3-3xy^2)/(x^2+y^2) has zero Gaussian curvature everywhere, except at the origin! To check this is a bit laborious, you have to compute Z_xx * Z_yy – Z_xy^2, and check it is zero. I did this with the help of symbolic software. But if you plot the function, you can see it is a kind of curled conic: It is a ‘ruled surface’; it can be built up of straight lines emanating from the origin. I then realised that any such surface in fact has zero Gaussian curvature, so this whole thing really has nothing to do with the Monkey saddle. The point at the origin turns out to be hyperbolic; it has negative Gaussian curvature; the sum of the angles meeting in that point is greater than 360 degrees. To regularise the point in the origin, I added an ‘ordinary’ conic Z=sqrt(x^2+y^2), which has positive Gaussian curvature at the origin. With the right superposition of these funcitons The function plotted is " Z = (1/3)*(x^3-3xy^2)/(x^2+y^2) + 0. 0.58852869sqrt(x^2+y^2)"



Photo Photo


 5 comments
Roice Nelson:
+Gerard Westendorp , you may find this talk by Chaim Goodman-Strauss interesting as part of your investigations.
youtube.com - Math Encounters -- Shaping Surfaces
//www.youtube.com/watch?v=0av77zpBeH8>
Gerard Westendorp: +Roice Nelson Nice video, I like the bit that he cuts out the edge of a lettuce leave. I have their book too, Symmetries of things. Does 'Gatherings for Gardner' stiill continue? Roice Nelson: +Gerard Westendorp , yes it is still very healthy, with gatherings every two years in Atlanta. The next is in spring 2018. Would you be interested to attend? I'd be happy to write the organizers and recommend an invite for you. If so, shoot me an email at roice3@gmail so we can plan a good intro.
12 plus ones

02-Jun-17
I am trying to fold an approximation of a C1 isometric imbedding of an Euclidean torus. That is, fold a torus from a flat piece of paper, with no sharp folds.
But first, some easier fun. Fold a sine wave into a milk karton.


Photo

Comments:
 Roice Nelson: I like that you investigate mathematics with physical objects :)
17 plus ones

10-Apr-17

Conformal checkerboard Mandelbrot

Conformal checkerboard renderings of the iterated complex functions:
z_1 = z z_i+1 = z_i^2+z
So this starts with the identity function, and gets closer and closer to the Mandelbrot. I break the iteration if |z| > 2.
For the first few iterates, I do 'fractional iterates': alfa*z_i + (1-alfa)*z_i-1. This is to do a more gradual transition.

Animated Photo


Comments:
 Adam Majewski: https://commons.wikimedia.org/wiki/File:Mandelbrot_set_-_multiplier_map.png
6 plus ones

10-Apr-17
More fun with conformal checkerboard Madelbrot.

Photo


Comments:
 Refurio Anachro: ?I completely forgot about checkerboards!
3 plus ones

10-Apr-17
My previous post was an animation, this one is just a picture. A bit more relaxing to watch.

Photo


4 plus ones

11-Mar-17
I made this hinged polyhedron from lasercut parts. The hinges are still a bit loose, but it works! The polyhedron transforms from a icosadodecahedron to a rhombic iscosadodecahedron. In between, it is also a snub dodecahedron.

Animated Photo


Comments:
 John Baez: Wow! How are you changing its shape here?
Gerard Westendorp: +John Baez Thanks! Basically there are 2 ways to suspend the structure. If you suspend it by the top, the rest kind of drops down in the most expanded state. If you suspend the structure by lower points, it contracts under gravity. So it is normally suspended in the contracted state, and I pull a string to transfer to the other suspension mode.
John Baez: Nice!
17 plus ones

26-Oct-16
This is next level cool!

Photo

Kinematics Dress by Nervous System - 3D Printed by Shapeways
Roice Nelson: I got to see these two at a recent /Illustrating Mathematics/ workshop. They do really cool stuff!
And I mention the workshop because you should consider joining the next one :)
https://icerm.brown.edu/topical_workshops/tw16-1-im/
http://illustrating-mathematics.org/
4 plus ones

14-Oct-16

A Christmas version of my stereographic projeciton lamp.


Photo


7 plus ones


06-Aug-16

Fundamental polygon of the small cubicuboctahedron

This photograph is of the *fundamental polygon* of the small cubicuboctahedron. If you fold the edges of this polygon together so that a closed surface is formed, it should be a surface of genus 3. This is following up on the idea that 'star polyhedra secretly are higher genus surfaces' in my previous post The small cubicuboctahedron,has 6 octagon slicing through it. It is related to the Klein Quartic, it has 24 vertices (KQ has 24 heptagons), and it also has genus 3. I want to make an animation of the small cubicuboctahedron warping into the genus 3 surface.

Photo


6 comments
John Baez:+Owen Maresh - My aforementioned page explains the relation between the cubicuboctahedron and a tiling of the hyperbolic disk.
Gerard Westendorp:+Owen Maresh The hyperbolic tiling of the Poincare disk is actually shown on the Wikipedia page for the small cubicuboctahedron. I don't know much about modular forms, but I suppose you could just construct a complex function by putting poles and zeros on the vertices of the tiling, and then solving Cauchy Riemann.
Gerard Westendorp:+John Baez Yes, on the Wikipedia page for the small cubicuboctahedron there is a reference to a page dy D. Richter. He "paints" an (8,3,8,4) pattern on the (7,7,7) pattern of the hyperbolic disk. You can also reverse this, paint a (7,7,7) pattern on the small cubicuboctahedron, and get a genus 3 surface tiled by (7,7,7), which also has the correct number of faces, vertices and edges. I thought that was cool and started making an animation. But as you remark, it will not yield the correct Klein Quartic. The point is, there are more than one ways to glue toghether the fundamental polygon into a genus 3 surface. All of these seem corect at first, but you have to check the "eight-fold way". (Remember Jos Leys had to correct his fist version of the gluing animation, after Henri Segerman remarked that he should "twist" more before glueing)
12 plus ones

31-Jul-16
I have always been a bit puzzled about the fact that uniform star polyhedra (https://en.wikipedia.org/wiki/List_of_uniform_polyhedra) have Euler Characteristic not equal to 2. (If you don’t know what Euler characteristic is, it it worth knowing!). This means that these polyhedra should in some way be related to higher genus surfaces, but you don’t see any holes, like with the doughnut with genus 1 and 1 hole.
If you look at the list of uniform star polyhedra, the simplest case should probably be the so-called Octahemioctahedron: A cubocahedron with the squares removed, and replaces by inter-slicing hexagons. This one has genus 1, it should secretly be a torus.
I have now figured out the relation. In the animation, watch the purple vertices. They move through the surface, so that it warps between a tiled torus and a Octahemioctahedron.
So in effect, uniform star polyhedra are in fact tilings of higher genus surfaces, but the holes are hidden by the intersections of the surfaces. You may be able to do a similar animation with all uniform stars. Bit of work though…

Animated Photo


Comments:
 Henry Segerman: I think there should be a way to see the star polyhedra as branched surfaces, and then the https://en.m.wikipedia.org/wiki/Riemann–Hurwitz_formula applies.
\Gerard Westendorp: +Henry Segerman
Another way to see that star polyheda are secretly tilings on higher genus surfaces, is to draw a fundamental polygon on the hyperbolic tiling with the same vertex structure. For example, here it is done for the small cubicuboctahedron: https://en.wikipedia.org/wiki/Small_cubicuboctahedron From there, you can make a donut shape, as the recent animations by Jos Leys show.
12 plus ones

25-May-16

From stereographic projection to sphere inversion

I learned a while ago that a #stereographic projection of the Riemann sphere on the plane can be viewed as a #sphere inversion in a sphere 2X as big as the Riemann sphere. But that means that you can generalise to projecting bumpy 3D objects rather than just the Riemann sphere, obtaining a bumpy landsacpe rather than the complex plane.
This particular shape is a "uniformised hyperbolic dodecahedron". That is, the Gaussian curvature has been made constant everywhere (by a circle packing algorithm) except in the 12 cusps, where 10 triangles with 18 degrees angle meet. At the cusps there is positive Gaussian curvature, so that the rest of the surface has constant negative Gaussian curvature. The sphere inversion has been adapted a bit so the inversion sphere coincides with 3 cusp. The resulting picture has been rendered so that it looks a bit like #Philae on comet Churyumov–Gerasimenko

Photo


Comments:
 John Baez: Nice!
9 plus ones

18-May-16

Magnetic gear, made of Magnetix bars.


Photo

MagneticGear
6 plus ones

07-May-16
Originally shared by Arioch The - 1 comment
http://i.imgur.com/vPr8dTY.gif

Animated Photo


13 plus ones

11-May-16
From the animation of that cool hinged garage gate (https://plus.google.com/100749485701818304238/posts/NKYDbteHZk6), I constructed a hinged tesselation. It is similar to a well known hinged tessleation of squares, but the expansion in the Y-drirection is constrained, so that the squares buckle.

Animated Photo


6 plus ones

03-Feb-16

Klein Quartic 2D to 3D warp

This isn't a nice version yet of my "Klein Quartic 2D to 3D warp", but the first “prototype” is perhaps also interesting. I now have all 336 triangles of the 2D and 3D shape in a mutual map. There are 211 vertices, which fuse into 164 vertices when glued into a closed 3D shape. The simplest way to warp is to just do a linear interpolation of the 211 coordinates between the 2 states. That’s this thing here. Now I should think of how to do it nicer, smoother, better camerawork…

Animated Photo


Comments:
 Driss Moukaouame: Une trâme interéssante. Le passage en 3d peut être interéssant...
16 plus ones

09-Jan-16

Lasercut Pythagoras theorem jigsaw

I made an lasercut jigsaw of Pythagoras theorem. The 5 pieces fit in either the large square or the 2 small ones, because according to Pythagoras the Area's are equal. The puzzle is actually surprisingly difficult,. Often it takes people several minutes. I guess I am too late for the X mas buying frenzy, but I put this puzzle in my Etsy shop: https://www.etsy.com/nl/shop/GerardWestendorp

Animated Photo


12 plus ones
I embellished my laser cut Pythagoras proof jigsaw with some lasered engravings.

Photo


8 comments
Gerard Westendorp: +Lutz Donnerhacke
I mean an animaiton *in which* the triangle is varied.
Lutz Donnerhacke: +Gerard Westendorp Yep.
Gerard Westendorp:
Got the animation: https://plus.google.com/100749485701818304238/posts/SoVh1nv1pE6
5 plus ones

24-Mar-16

Animtion of Pythagoras proof used in Puzzle

Yesterday I posted a photograph of a jigsaw of a Pythagoras proof. To further illustrate that the proof works, I made this animation. As posted by +Refurio Anachro, (https://plus.google.com/+RefurioAnachro/posts/XkPLmdczcEq) the proof is related to the proof by Henri Perigal, who died in 1898, and had his proof carved on his tombstone! (see https://plus.maths.org/content/dissecting-table) Interestingly, you can *tile the plane* by the diagram of this proof. I am not sure this is well known, but it is cool. Note that the plane is tiled by an equal number of squares a^2 and b^2, (such tesselations are quite common on kitchen floors etc) and from this tessellation we can construct a tessellation with c^2 that also tessellates the plane. That proves Pythagoras. Then shift a b^2 square so that the red-lined section is formed, this is the construction used in the jigsaw. I got the diagram used in the jigsaw from a wikimedia file: https://upload.wikimedia.org/wikipedia/commons/c/c9/Academ_A_jigsaw_puzzle_depicts_the_Pythagorean_theorem.svg

Animation of Pythagoras proof 


PS: I also made this website. on this subject

4 comments
Owen Maresh:
I would like to believe that there's an identity of the Jacobian theta functions which can be related to this depiction. (because they have roots in lattices) Gerard Westendorp:
+Owen Maresh
Yes, maybe some connection with modular forms, elliptic curves, Fermat... Owen Maresh:
+Gerard Westendorp :
I was thinking specifically about the identity of theta nulls theta4(0,q)^{4} + theta2(0,q)^4 = theta3(0,q)^{4} here.
I was sort of extrapolating to what we'd see if you go from 0 green to all green, and the fact that at the beginning which is not part of the above, you have four-valent vertices -- that could easily correspond to the fourth power of something, and as the Jacobian theta functions on their complex plane have their roots in a lattice, that seems like the thing to do.
My first thought (related to +Tom Cuchta elsewhere) was:
how about we change each of the q/tau/k of each one of the factors -- the fourth powers written factored
(theta_4(0,q) theta_4(0,q) theta_4(0,q) theta_4(0,q)) + (theta_{2}(0,q) theta_{2}(0,q) theta_{2}(0,q) theta_{2}(0,q) = (theta_{3}(0.q) theta_{3}(0.q) theta_{3}(0.q) theta_{3}(0.q))
so one gets four columns:
change each one of the $q$ to correspond with the way that the four valent vertices at the beginning and end split into vertices connecting the middle of edges (I don't know how much offsetting of z is necessary).
Since the above is an identity, the idea is at the beginning and end we have it, but in the process of a movie, we'll want to see something like the difference or maybe the quotient minus the exp of the difference.
16 plus ones

24-Dec-15
Originally shared by John Valentine - 3 comments
*A repulsive image* with a soft circular constraint.
A few thousand points are arranged randomly, then allowed to repel each other. Some points are bigger than others, so they push harder.
There's no optimisation here, and it needs tuning for different initial conditions, so I'm not providing the link yet. It took about a minute to settle on a modest computer (1 thread in JavaScript in Chrome).

Photo


7 plus ones

19-Dec-15

Carpenter's Pyhagoras proof

I turned my "Carpenter's Pyhagoras proof" into an animation.

Animated Photo


Comments:
 Gerard Westendorp: In case you feel like a puzzle: What is the proportion of the squares given that exacly 3 out of 8 boards are cut diagonally?
13 plus ones

04-Dec-15

Generating cycloids and trochoids from intersecting a ruled surface with a plane

I found out that you can generates cycloids and trochoids from intersecting a ruled surface with a plane. This ruled surface is generated by connecting the upper and lower circle of a cylinder with lines. Connect point {cos(a), sin(a), 1} with point {cos(Na), sin(Na), 0}, for a large set of {a}. Then the intersections of these lines with a horizontal plane have the form {A cos(a) + B cos(Na), A sin(a) + B sin(Na)} This is just the form for cycloids.

Photo


11 plus ones

24-Nov-15
Yesterday I saw a post by Henri Segerman (https://plus.google.com/+HenrySegerman/posts/Umf7DjAzJhZ) about the 'jitter box'. I have quite a collection of related stuff myself, that I have not made public yet. Here for example is an animation of a dodecahedral hinged polyhedron. I have cardboard prototypes of it, and I am working on some lasercut prototypes too.
Note that this construction transitions between 3 different Archemedean solids: icosadodecahedron, snub dodecahedron, and rhombic dodecahedron.

Animated Photo


15 plus ones

15-Nov-15

Jacobi elliptic function

A Jacobi elliptic function. This time The checkerboard pattern is animated only over magnitude, not phase, so that the squares appear to originate from the poles and absorb in the zeros. Jacobi elliptic funcitons have a 2D grid of poles and zero's.

Animated Photo


Comments:
 Owen Maresh: In the near future there'll be a realtime touch interface which will display all twelve Jacobian elliptics, the four Jacobian theta functions as functions of q or k or the half period ratio Driss Moukaouame: Je ne sais pas encore poser du carrelage de cette façon. La périodicité et la similitude qui sont appliquées au motifs me semble interéssante.
Gerard Westendorp: +Owen Maresh
Sounds cool!
24 plus ones

13-Nov-15

Riemann Zeta function

Conformal checkerboard coloring of the Riemann Zeta function. See the points that appear to absorb all squares? They seem to lie in 2 lines... If you can prove that, you will get 1 million dollars, and be famous (it is the Riemann hypothesis).
By the way, I found a weblog of Fritz Mueller who made similar pictures: http://blog.fritzm.org/2011/08/moebius-transformation-animated-gifs.html But he starts from a checkerboar, and then Mobius transforms it, so it is not quite the same.

Animated Photo


4 comments
Gerard Westendorp:
+Refurio Anachro You can find the real axis from the lines of zero's, and a pole at z=1. (The box is from (-25,-5) to (5,25)) I am not rally an expert of the Reimann zeta funciton, but I don't think it is singular on the real axis. At least my numerical routine gives fairly ordinary looking values.
Refurio Anachro:
You're right Gerard, Riemann's zeta has no such line. I should have known, and I am feeling a bit silly. Looking at a full phase plot helped:
https://en.wikipedia.org/wiki/Riemann_zeta_function
I think I'll come up with an example shortly.?
Refurio Anachro:
Okay, maybe not today. As you probably know, conformal mappings allow to distort the complex plane, to make a circle from a square, fold a side of a square inside to make a triangle, or make an upper-half-plane model, or fold that again to only get a horizon-ray. And, of course, much other stuff.
That folded upper-half-plane seems a bit contrived, and there sure is some more canonical or prominent example. The half-plane itself is beautiful, but maybe too popular to be sexy.?
20 plus ones

30-Oct-15

laser cut cycloids

This set of laser cut cycloids runs quite smoothly. I might modify it slightly, so that it is suitable as a gadget.

Animated Photo


7 plus ones

30-Oct-15
Laser cut cycloids, from acrylic. I've wanted to make rolling cycloids for a while, thought of 3D printing, but decided laser cutting is probably better.

Animated Photo


10 plus ones

25-Oct-15
Klein Quartic laser cut from wood. Could be used as a potholder

Photo


11 plus ones

07-Sep-15
I came accross a nice video by Jack van Wijk, about 'regular maps'. (http://www.win.tue.nl/~vanwijk/regularmaps/regularmaps2009.wmv) These are regular tilings of closed surfaces, like Klein's Quartic. But there are many more. But this is the fist time I see so may pictures of them.

Photo


5 comments
Gerard Westendorp:
+Jack van Wijk
Looks great! I will see if I can understand your article, so far it looks very readable. Do you have by any chance the object R19.23 ({7,7}). That would fit in beautifully with our Golay code quest:
https:
//plus.google.com/100749485701818304238/posts/fJX43yhNuyZ Jack van Wijk:
No, I don't think I have got that one. I have to check with my software, but I guess I would have it included in the video and the paper if I had. My approach is far from exhaustive, it is still a surprise to me when I have a hit and when not. Btw, the real highlight in my last round is R7.1{3,7}, aka as the genus 7 Hurwitz or Macbeath surface.
Gerard Westendorp:
+Jack van Wijk I think I made a mistake:
The genus 19 {7,7} object has 24 heptagons, I thought it was 12. But then it might not be as relevant. R10.9 :
Type {4,7} would be better, it gives the data/parity relation for Golay in a checkerboard fashion.
7 plus ones

07-Sep-15
This picture is a figure with 24 heptagons, it has 2*168 sub triangles, just like the Klein Quartic. But it has 42 vertices instead of 56, and its genus is 10 instead of 3. The outer heptagons are split into small wedges, each occurring 7 times as a 1/7th heptagon, they are implied to be glued together. The figure arises in my description of the Golay code, where each databit had 7 parity bits associated with it, and vice versa. If you picture the databits on the green heptagons, then the blue are the parity sum of its neighbouring heptagons. I was a bit puzzled first that these strange figures exist, but I found out there are many more. I found a phd thesis on it: purl.tue.nl/727425851426839.pdf The thesis gives a table of ‘regular maps’, and the one I give here is listed among them. Some maps in the table have names, but this one does not.

Photo


7 comments
Gerard Westendorp:
+Roice Nelson
Thanks! Btw, I meant to write "42 *vertices* instead of 56. I edited the post to correct this. Gerard Westendorp:
+John Baez
Thanks! I did think about the Euler characteristic. But that alone is not sufficient to guarantee a Platonic tiling, as I found out years ago after making a cardboard model of a genus 2 object tiled with 12 heptagons. John Baez:
Right, I don't know when the Platonic tiling actually /exists/.
8 plus ones

04-Sep-15

Stellated Klein Quartic

While thinking about my previous post (Golay codes) I ran into a *Stellated Klein quartic*. One way this is related to my previous post is that you can "stellate" the dodecahedron into the great dodecahedron by extending the planes until they reintersect. You then still have 12 faces and 30 edges, but the number of vertices has shrunk from 20 to 12. This means the Euler characteristic goes down by 8, so the great dodecahedron has genus 4. You do not see the holes, but there may be a way to warp the surface so that you can. Just like the dodecahedron, you can also stellate the Klein Quartic. You can do it is several ways, the one in the picture extends each heptagon into a heptagram, such that the new vertices end up in the centres of the faces. You get a figure with 24 heptagrams, and at each vertex now 7 heptagrams meet. Again, the number of faces and edges stays the same, but the number of vertices goes from 56 to 24, and the genus goes from 3 to 19! Another way this is related to my previus post, is that the number of parity bits a data bit is related to is 7, and vice versa, each parity bits has 7 data bits it related to. If you interpret the bits as vertices, and the relations as edges, you get some figure with 24 vertices and 84 edges. You could use the dual, so that you have 24 faces, each with 7 neighbours. But in both case, you do not quite have the Klein Quartic. What I suspect is that you have a kind of stellation of the Klein quartic. I believe it a figure with (7,4) tiling with 24 hepatgons, and genus 10. I am trying to construct a picture, but in the mean while, I found this one, which is also quite nice. If you stellate the dodecahedron, the symmetry group remains the same, you can still tile it with a regular pattern of 60 black and 60 white triangles. This is also true for the stellations of the Klein quartic.
I only displayed 15 of the 24 heptagrams.

Photo


4 comments
wendy krieger:
Not all of the polygons do. There is a limit of size on when the edges diverge.
So you can't make 7/3 out of these heptagons.
Coxeter wrote about it in 12 Essays - the Bueaty of Mathematics, Gerard Westendorp:
+wendy krieger
With 7/3 do you mean stellated heptagons which connect vertices of the ordinary' heptagon like 1,4,7,3,6,2,5,1? wendy krieger:
That's how it works.
8 plus ones

26-Aug-15
This is a post to explain how to make rolling cycloids, with the outer and the middle cycloid standing still. (See for example, https://plus.google.com/100749485701818304238/posts/6UMwHbZTnou). Referring to the figure, we have 5 circles, a circle of radius N, N-1, N-2, N-3, N-4 (red, blue, black, magenta, green). At t=0, the circles are arranged so that they touch in a special alignment, that is probably clear from the picture. This alignment ensures that the black circle is centred on the red centre, as is the green circle. Now we start rolling the blue circle, and inside it the black one. We can choose the rolling rate of the blue circle, but the black rolling rate needs to be coupled to the blue rolling rate in such a way that its centre does not move. The Magenta circle can now roll inside the black one, at a rate that we can still choose later. But again, the green one needs its rolling rate to be coupled to the magenta rolling rate so that it remains centred. OK, so now we have the circles rolling, with the black and green ones centred with the red one. To make the cycloids, just choose a point on a circle, and trace out its path relative to the circle in which it rolls. That will be a cycloid. We then get a set of rolling cycloids, with the middle one still centred, but not necessarily stationary. To make it stationary, remember we were still free to choose the rolling rate of the magenta circle. We can use that degree of freedom so that the green cycloid stands still. This picture shows hypocycloids, but the epicycloids work the same way. In fact, I only have to change on minus sign in the code for the cycloids to flip from hypo- to epi-.

Photo


5 plus ones

24-Aug-15
Like the previous animation, but now hypocycloids, rather than epicycloids. The principle will work for any consequetive range of cycloids.

Animated Photo


Comments:
 Juke Westendorp: Cool!! John Baez: Nice!
10 plus ones

18-Jul-15

Getting data From Pluto

One of the most amazing things when you think about the pictures from Pluto, is how do they send these pictures all the way be back to earth? The antenna on the spacecraft is only about 100 Watt. While seeing the entrire (dwarf?) planet Pluto with a telescope in visible light is barely possible, this 100 Watt radio signal can actually send us these sharp photographs.
I will summarise a little exercise I did on this. (I do only very rough estimates, I just want to understand the basics. Still, I am known for extreme sloppiness…)
Pluto is 4 light hours away, about 4e9 km. Its antenna can aim a narrow beam of radio at an angle of about 0.3 degrees. So by the time its signal reaches earth, its radio signal will have spread out over a radius of 3.6 million km. The power reaching the 70 meter parabolic dish is only 4e-14 watt. That’s not much. You can amplify it, but then you amplify also noise. How much noise? Well, we famously know there is 4 Kelvin microwave background, so using Stephan Boltzmann, there should be 5.6e-8*4^4 Watts per square meter of power, about 3 milliWatts on a 70 meter deep space parabolic antenna dish. That seems bad, there is about 1e11 times more noise power coming in than the signal from our little baby. Luckily, the parabolic dish is extremely direction sensitive. The 4K blackbody radiation is coming from all directions, but the 70 meter Deep Space network parabolic antenna can pick out something like 1 arc second, or 1/3600 degrees. Only a factor 7000 to go for the signal to noise ratio. The remaining signal to noise ratio improvement comes from narrowing the radio frequency bandwidth. The microwave noise is spread out over a frequency range of about 1e11 Hz (Using hf_max ~kT). So if you look at a very narrow band, of only 10 kHz or so, the signal to noise ratio goes up by a factor 1e7. That is enough, by a couple of orders of magnitude.
One consequence of the narrow frequency band is the slow communication. It is not just that there are no good internet providers on Pluto, you cannot send any faster than the frequency band, which is only a few kilohertz.
Couple of interesting things: The earths atmosphere is transparent to these microwaves, although the frequency they use is quite close to the microwave oven frequency (~2GHz), which would be strongly absorbed by water.
The error correcting algorithms they use are really cool. The coolest are “Golay codes”, which use 24 bit blocks, and trick for correction using symmetry groups in 24 dimensional space, like M24.
Wikipedia image
John Baez: It's great how physics combined with tricks like the Golay code get the job done. There's a lot of 'hidden' science and math behind those Pluto pictures.
2 plus ones

30-May-15
Originally shared by Industry Tap - 11 comments
*Copper Wire. 1 Battery. 2 magnets.*

Animated Photo


Comments:
 Gerard Westendorp: As I commented on the original post, I think there is basically a permanent magnet, and an electromagnet. I think the elctromagnet shoud always be slightly ahead of the permanent one (assuming it is of opposite polarity)so that it will pull it foreward. It would seem the current device could be optimised by some trick that makes the electric contact points ahead of the magnets.
2 plus ones

24-May-15

Tensegrity chair.

The idea of #tensegrity is that the "compression" bars do not touch, due to the tension in the cables. There is a nice way of making a tensegrity icosahedron with 6 bars.

Photo


11 plus ones

11-Feb-15
I am doing a project on generalisations of cycloids. This is the first result, it contains cycloids on a sphere, which fit together like gears.

Animated Photo


16 plus ones

27-Jan-15
I tested some bright green LEDs on my stereographic projection lamp. In the background a cardboard model of Escher´s relativity I made while recovering from an operation.

Photo


Comments:
 Jeroen Cappendijk: Hi Gerard, Hoe gaat het nu met je? Gerard Westendorp: +Jeroen Cappendijk
Ha Jeroen. Zo als je ziet probeer ik mijn wiskunde een natuurkunde hobby te combineren met de rest van mijn leven. Als ik Facebook moet geloven, zit jij veel op tropische eilanden met een hot chick...
9 plus ones

03-Oct-14
An improved version of a LED lamp with 3D printed dodecaheral ball. The idea of using a point source LED as kind of stereographic projector has also been done by Henri Segerman.

Photo


6 plus ones

06-Sep-14
This planetary gear with epicycloids and hypocycloids is a nested version of the 2 previous ones. You could continue theis sequence to larger wheels, but the next level, with 16 octagonal planets, has overlapping planetary wheels.

Animated Photo


one plus one

06-Sep-14
Planetary gears built from epicycloids and hypocycloids

Animated Photo Animated Photo


no plus ones

03-Jul-14
My latest 3D prints.
4 Photos - View album

Comments:
decor light: Good afternoon. It is interesting and can be used to form molding? You use plastic? What machine work?
Gerard Westendorp: +decor light Thanks for your reaction. These designs are 3D printed using a material that shapeways calls "colored sandsandstone": https://www.shapeways.com/materials/full-color-sandstone In future, higher resolution might be possible with new materials.
My 3D designs: https://www.shapeways.com/shops/thinking
decor light: +Gerard Westendorp Your toys can be heroes new cartoon or puppet shows if they do manageable.) Very interesting technology and your work.
6 plus ones

27-Jun-14
#geometry #lego Here is a Lego version of the Carpenter's Pythagoras proof. The Red/White region has the area of the yellow and blue squares, but also equal to the area of the cyan square. If you like integers, you can apply Pick's theorem.

Photo


one plus one

20-Jun-14
Looking forward to to get these 3D fractals outof the 3D printer. They will be made from colored sandstone.

Photo Photo


2 plus ones

13-Jun-14

New 3D prints!

http://www.shapeways.com/designer/Gerard_Westendorp

Photo


4 plus ones

25-Apr-14
Originally shared by Roice Nelson - 1 comment


Photo


one plus one

16-Apr-14
Hmm, Google plus... Maybe I'll use to talk about physics and maths.
no plus ones

16-Apr-14
Homepage Gerard Westendorp Homepage Gerard Westendorp westy31.nl
no plus ones


A laser-cut hinged polyhedron. The hinges can be 'snapped' to the faces, allwing for fast assembly.

Photo

My webpage on this
Comments:
Roice Nelson: These are awesome!
9 plus ones


*Hinged polyhedra* have made a come-back on my priority list. In this animation, the ‘hinged icosadodecahedron’ morphs between: icosadodecahedron snub dodecahedron rhombic dodecahedron compound of icosahedron and great dodecahedron great ditrigonal icosidodecahedron And some strange “retrosnubs”...
For the non-intersecting part of the sequence, a mechanical model is possible. (I have several). But recently, I decided to look at the intersecting part too.

Animated Photo

My webpage on this
Comments:
 Boris Borcic: the icosahedron being the convex hull of the great dodecahedron, I'd expect their compound to be dull.
Gerard Westendorp: +Boris Borcic Well, thats what the hinges form...
17 plus ones


I like this video. Worth watching if you care about the truth on infinite sums and the Riemann zeta funciton.
https://www.youtube.com/watch?v=YuIIjLr6vUA

Photo
Comments:

Comments:
Numberphile v. Math: the truth about 1+2+3+...=-1/12
Niles Johnson: I liked this too. And I liked the Numberphile video! I'm amazed at how much this issue has roiled the mathematics corners of YouTube.
Gerard Westendorp: +Niles Johnson Remarkable that the Numberphile clip got 6 million views. This is stuff that is really worth understanding, the Riemann zet function, infinity, Ramanujan sums, ...
6 plus ones

Collapsible hinged tessellation in action.

There might be a relation to number theory: Each square has 2 numbers (i,j). Let these correspond to the coordinates of the horizontal plane that the centre of the square has at the most expanded state. We can normalise them to the integers. The centres of the squares move as (sin(alfa)+cos(alfa)) * (i,j), where (alfa, -alfa) are the alternating rotation of the squares. So if a square centre exactly overlaps an integer point in is movement back to the origin, then (i,j) are not relative primes. So this thing is a relative prime detection machine.

Animated Photo

Jon Eckberg: Yes!
18 plus ones

The 5X5 version.

Animated Photo


12 comments
Gerard Westendorp:
+Jon Eckberg In a reply of the post linked below, I put photo of an actual working model. It is pretty close to collapsing all the way. Maybe exact is possible, if you turn the hinge connecting 2 heights into a kind of crankshaft that uses the space outside the 3X3 square. (You probably can't follow me here, I would to draw or build it rather than try in words...) plus.google.com - I don’t think anyone noticed yet that if you continue transforming the hinged...
Owen Maresh:
Also, what happens to, say, hyperbolic tilings? Owen Maresh:
And, does the infinite limit work?
16 plus ones


Klein Quartic shirt

I realised yesterday that a Tshirt, with an inner lining sown in, (So it has 2 layers) is in fact a closed genus 3 surface. This offers the possibility of making a Klein quartic Tshirt, ie tiling the whole shirt with 24 heptagons.
As a warming up exercise, I dressed up this little doll with a genus 3 surface: It consists of 4 octagons.
Take 4 2N-gons, stack them facing up-down-up down. Then glue together the even edges of layer 1 to layer2, and layer 3 to layer 4. Then glue together the odd edges of layer 2 to layer 3, and layer 1 to layer 4. You will get a Platonically tiled surface of genus N-1. So 4 squares make a torus, 4 octagons make a genus 3 surface.

Photo


9 plus ones



Klein Quartic on a cuboctahedron.

In the process of trying to map a Klein Quartic pattern on a joined inner+outer Tshirt, I found an interesting embedding of the Klein Quartic on a cuboctahedron-like shape.
It is an inner cuboctahedron glued back-to-back to an outer cuboctahedron, each with 4 of the 8 triangles removed. This gives a genus 3 figure, each vertex has faces (4,4,3,4,4,3). So it could be considered an Archimedean tiling of a genus 3 surface. On its surface, I mapped the Klein Quartic. The 24 heptagon centres: 3 on each of the 8 triangles. The 56 triangle centres: 4 on each of the 12 squares, plus 1 on each of the 8 triangles.

Photo

Comments:
 Arnaud Chéritat: Amazing!
Roice Nelson: Reminded me of a polyhedral model I've seen based on nested icosahedra. See figure 1a in this paper by Carlo Séquin.
https://people.eecs.berkeley.edu/~sequin/PAPERS/2007_Bridges_HyperbolicTiles.pdf
Gerard Westendorp: +Roice Nelson
I spent about a day trying to convert the cuboctahedral model into an icosahedral one: Simply split the squares into 2 triangles, and stretch/skew them a bit into equilateral triangles. I thought this would move things towards lest twisted heptagons, until I realised that this works for the one side, the other side actually gets ‘more’twisted. So I decided not to continue that model.
The one in the picture of Carlo Sequin's article is ‘locally’regular, but not globally, as Carlo Sequin calls it. But the pattern is a lot less twisted. Thanks for the link by the way!
10 plus ones

Next step in my project to make a Klein Quartic T-shirt. I have now embedded the 24 heptagons on 4 octagons, which form a genus 3 surface. Next, I need to deform it to something wearable. Also, maybe I will figure out an algorithm to warp the 168 sub-triangles as smoothly as possible over the surface.

Photo


12 plus ones


Klein Quartic shirt

Anoter phase in the design proces of a Klein Quartic shirt. Printed on paper before moviong on to textile. It has the 24 heptagons wrapped around the surface of the shirt, including the inner side of the shirt. A shirt surface has genus 3, but the heptagons have to be quite severely deformed.

Photo

Comments:
Roice Nelson: Awesome, love it :D
Maris Ozols: I wonder if there is a mathematically minded designer who could help you to turn this into an actual wearable shirt. One person who comes in mind is Holly Renee who designs science-themed dresses: shenovafashion.com - Shenova Fashion
Gerard Westendorp: Wow, these look pretty cool! Although these ladies look as they don’t wear the same size as me… Maybe I will contact them.
One thing that still bothers me a bit is whether to switch from a ‘globally regular’ tiling to a ‘locally regular’ tiling. The latter is still a tiling by 24 heptagons, but lacks certain global symmetries, so that is not the correct Quartic. However, the heptagons become a lot less twisted.
15 plus ones

Happy 2018



Animated Photo


Comments:
 John Baez: Happy New Year to you too!
10 plus ones

Bezier triangles

I ran into *Bezier triangles*.
They are quite a cool way to turn a coarse triangulation into a smoothed deformed surface. Bezier and de Casteljau invented Bezier curves when they were working at Renault and Citroen on defining the precise shape of car designs. You can generalise Bezier curves to 3D triangles. The points on the triangle are a weighted sum of the vertices, and the “control points”. The weights are chosen so that they have nice properties, such as the fact that the edges of the triangles are Bezier curves. Also, it is easy to obtain mesh points from them.
The animation is an icosahedron on which control points (red spheres) on the edges are moved around.
Wikipedia on Bezier triangles:

Animated Photo 


15 plus ones


Yesterday I was at a Dutch Mathematics & Art symposium. Amongst a lot of other cool stuff, one interesting thing I saw was some work by Melle Stoel. He is creating sculptures by gluing together antiprisms. If you glue together 2 antiprisms, the “main faces” end up at an angle. You can choose this angle by varying the height of the anti-prism.
I used this idea to make a polyhedron, in this case the buckyball. Some more stuff by Melle Stoel: http://gallery.bridgesmathart.org/exhibitions/2014-bridges-conference/mellestoel

Photo


14 plus ones


Another example of the antiprism trick of my last post: 6 antiprisms form a cube on the inside, cuboctahedron on the outside.

Photo


12 plus ones



While working on yet another Klein Quartic project, I got side tracked into making this mechanical model of Greg Egan’s “inside out” Klein Quartic. The flexible parts are a bit short; they almost tear apart when doing this movement.

Animated Photo

Hugo Tadashi Kussaba: Awesome! Are you going to share the instructions to build this fascinating model? :) Gerard Westendorp: +Hugo Tadashi Kussaba
Thanks! I will put the instructions online, but I saw there is a mistake in the coloring. Also, I'll make the flexible arms a bit longer. Should have that ready in 1 or 2 days.
20 plus ones

Version 3, some technical improvements. Also, I had a go at animating with invisible strings.

Animated Photo


10 plus ones


13-Jul-17
*"This sentence is either false or undecidable"*
The above sentence cannot be true, it cannot be false, but it also cannot be undecidable. Perhaps it can be "not even false"...
6 comments
John Baez:
+Timothy Gowers - in logic, "truth" is the last refuge of scoundrels. But these scoundrels often use "true" to mean "valid in some model of a formal system that I'm fond of, even if I can't specify it except by resorting to some other model that I can't specify any more clearly". (E.g. the "standard" model of Peano arithmetic.)
By this standard, the Goedel sentence is often considered undecidable but true.
I didn't even try to check the logic of +Gerard Westendorp s argument; I just wanted to see what happens if we replace "truth" with "provability". Timothy Gowers:
Indeed, the fact that statements can be both true and undecidable was what made me think that the statement "This statement is either false or undecidable" might be true and undecidable, but there are problems with that, since it seems to be quite easy to prove that that is the only possibility. Here's the proof:
it can't be true and decidable, since then it would be false; it can't be false, since then it is true; and therefore it must be true and undecidable. But since I've just proved that it is true, it isn't undecidable after all, and I've reached the end of the road. Gerard Westendorp:
I will follow Turing, so “undecidable” = “the algorithm to decide the truth value does not halt for this input”. ( I find Turing easier to understand than Godel.)
Suppose you are working for a company that computes whether sentences are true or false. Your boss, Boss_1, hands you a sentence, and you start computing, using your extremely advanced algorithm. Since you are nobody’s boss, you are called Boss_0. So every now and then, Boss_1 asks how you are going, so he can tell his boss, Boss_2, that either A:
the sentence is true, B:
The sentence is false, or C:
Boss_0 has not yet finished computing. Then, competitor EvilCorp sends in a sentence “This sentence is false.” So Boss_1 give it to you, and time passes away, while you are working on it. As time passes, Boss_1 begins to get nervous; you know what Boss_2 is like… What if Boss_0 *never* stops computing? So he does something revolutionary:
He starts thinking for himself! He figures out that indeed, your algorithm isn’t going to halt in this case, you he tells you to stop, and tells Boss_2:
“That sentence is undecidable”. So Boss_2 can proudly say to Boss_3, that the sentence from EvilCorp is undecidable by Boss_0, but that Boss_1 has figured that out in time. So then EvilCorp sends the message:
“This sentence is false, and Boss_1 can’t figure out that it is undecidable”. In the meanwhile, Boss_1 has learned to always check if a problem halts before giving it to Boss_0. But in this case… Luckily, Boss_2 intervenes, to say that OK, this sentence is not decidable by either Boss_0 or Boss_1, but that he, Boss_2, has decided that!
EvilCorp knows that your company has many layers of organisation, so they don’t want to recursively say that Boss_N can’t decide something. So they come up with “The Goldbach conjecture is false”. Before the sentence lands on your desk, Boss_1 has spent already a long time trying to figure out if it is decidable. But it was taking him so long that he thought, maybe I will give it to Boss_0, so that he can start working, and then if I later figure out that the problem is indeed decidable, we will have gained time. So Boss_0, Boss_1, and secretly also Boss_2 and Boss_N, are all working on this sentence. Boss_0 remembers he used to think that a million years is a long time, but maybe compared to the computation time of his present task it is actually very short…
I think the point is, as I think John Baez is saying, that the idea that a sentence *is* true, is too vague, you have to say for example ‘computable by a specific algorithm’. But, as Godel and Turing found, any sufficiently advanced algorithm has inputs for which it does not halt. Including an algorithm that tries to decide if other algorithms halts. So, there are some things we cannot know, but we do not know which things. (Wasn’t Kant trying to tell us that?)

11 plus ones

26-May-17

The Dirac belt trick

I’ve known about the Dirac belt trick for years, and I often did the Balinese cup trick with my favourite drink, which happens to be beer. I sometimes wondered, can you do the Balinese cup trick with some kind of mechanical device. Last week I was staring at the animation on the Wikipedia page: https://en.wikipedia.org/wiki/Plate_trick Although I was determined focus on another project, I was seduced into building a mechanical model of this thing. The animation here is a re-glued version of a failed attempt, so it is a bit messy, but it works.
I find it fascinating that you can rotate something by an infinite angle, without net twisting its connection to solid earth. On the animation, note the red tape around one arm. It rotates 360 degrees, while the cube with the Dirac portraits rotates 720 degrees. This is all related to the SU(2) thing being the double cover of our familiar rotation group SO(3). That’s described in a lot of web pages already. I want to make an animation of a Dirac wave packet, but when…

Animated Photo

Comments:
Kazimierz Kurz: Sorry but animation is unclear for me.
Gerard Westendorp: +Kazimierz Kurz Maybe I'll do a new one with numbers 1-4 stuck on the segments. Hopefully that might help.
10 plus ones

28-May-17
My previous post was perhaps a bit unclear. Here is a second attempt, better lighting and numbers attached to the sides of the “twisting” object.
One way to understand the movement is to first think of a torus formed by flexible hose. You can continuously “twist” this torus without actually twisting the hose relative to itself. So each segment of the hose is rotating relative to the earth around the local axis of the hose. (Instead of a flexible hose, you could use also a “kaleidocycle” http://www.mathematische-basteleien.de/kaleidocycles.htm ) But the hose itself does not get twisted, because 2 consecutive segments do not rotate relative to each other, they just need to flex a bit as a local part goes from an inner to an outer bend.
Next, imagine rotating this whole torus along an axis somewhere along the hose, with a rotation that exactly cancels locally the rotating of the hose, so that a one point, the torus is not moving relative to the earth. This will imply that at the opposite end, the hose will appear to rotate at twice the angular velocity as the hose rotation, while it is also swinging about the global axis just defined. This is really what this belt trick object is doing. It is a flexible hose, rotating about its hose-axis, but at the same time rotating (in the opposite direction) as a whole around a global axis going through the 2 points it is attached to the frame. Once you understand that, you can immediately figure out the movement on each point along the hose. In the middle, where the cube with Dirac’s portrait is, the hose is upside down, and aligned to the global rotation, so there the net rotation is 2 times the hose rotation. On the horizontal segments, you can see the hose rotation and simultaneously the global rotation.

Animated Photo


5 plus ones

13-Jun-17
I cut loose the central section of the cardboard Dirac belt trick device I talked about in my previous post. Now my arms have taken the place of the rest. If my arms and hands had enough hinges, I could do this trick without the cardboard device: Rotate a part indefinitely, while it remains connected to “earth”, with no net twisting of my arms.

Photo

Dirac
6 plus ones

31-Jan-17

N-dimensional circumsphere of an N-simplex directly from its Cayley Menger matrix

A one-page proof of a nice theorem: You can find the N-dimensional circumsphere of an N-simplex directly from its Cayley Menger matrix. In other words, you need only to know the distance between the points.
https://westy31.nl/Circumsphere/ncircumsphere.htm#Coxeter

Photo


5 plus ones

01-Jan-17

*Modular to Elliptic*

Ever since the proof of Fermat’s Last Theorem, the relation between modular forms and elliptic curves sometimes captivates me. (Disclaimer: I am not an expert on this!)
Both modular forms and elliptic functions can be thought of as being composed of symmetrical tiles on the complex plane. Each tile has a pole and a zero, which together completely determine the complex function. Modular forms have the poles on the real axis, precisely at the rational numbers. Each tile of a modular form corresponds to exactly one rational number. Elliptic functions have the poles and zeros on a regular 2D lattice. (For pictures, check out my website https://westy31.nl/Geometry/Geometry.html) Imagine the rational numbers on such a lattice, numerators and denominators being x-axis and y-axis respectively.
(For graphical purposes, the real axis of the modular form has been mapped to a circle.)
This animation morphs the tiles of a modular form to tiles such that the poles end up on a 2D lattice. The resulting tiles are actually not quite the tiles of an elliptic function, but perhaps interesting anyway. Firstly, only numerator/denominator points on the lattice that are relatively prime get a pole from the modular tiling, the others not. I marked these relative prime pairs as green circles, the other as white. Remarkably, the modular form ‘knows’ which integer pairs are relative prime. The tree-like structure which appears to emerge out of the modular tiling is called the Stern-Brocot tree. A cool property of this “Stern-Brocot tiling” is that no lattice point ever lies inside a triangle, they all lie exactly on a vertex, or if they are non-relative prime points, they lie outside the tree. Looking at a region close to the origin, this region outside of the tree gets squeezed into less and less available surface area as more generations of tiles are added, but the non relative prime points still remain outside the tree, on ever-narrowing “cracks” along directions (p/q). In the meanwhile, if you look at the entire tree, it gets bigger exponentially with the number of tiles, while the surface is filled up grows only as the square root of the number of tiles. Does this demonstrate that there are much more non-computable numbers than computable numbers? The area of each tile in the lattice configuration is ½. This can be seen with Pick’s theorem.

Animated Photo

Shava Nerad: I can't help think of this, I know the dimensionality is wrong...
youtube.com - Exotic Jellyfish
9 plus ones

30-Nov-16
A lamp I saw in the hague central station. Looks cool.

Photo

Comments:
Roice Nelson: Looks like it may be a honeycomb of truncated octahedra!
en.m.wikipedia.org - Bitruncated cubic honeycomb - Wikipedia Gerard Westendorp: +Roice Nelson Yes, I wonder how they made it. I guess you would need some efficient assembly technique, there are hundreds of these truncated octahedra.
6 plus ones

24-Nov-16

ultra-bright small LED

I managed to fix a new ultra-bright small LED into my stereographic projection lamp. This LED requires a heat sink, normally it is mounted on a printed circuit with conductive metal layers. But i thought thick copper wires will also act as a heat sink. It works!
I also use a flexible goosneck tube now. It's on Etsy: https://www.etsy.com/nl/shop/GerardWestendorp

Photo


4 comments
Roice Nelson:
Are you selling? I would buy one :)
Gerard Westendorp:
+Roice Nelson
Thanks! It's on Etsy:
etsy.com - by GerardWestendorp
//www.etsy.com/nl/shop/GerardWestendorp>
Driss Moukaouame:
Le résultat est très sympa..;)
17 plus ones

15-Oct-16

3D printed Pythagoras tree

This 3D printed Pythagoras tree switches the plane in which new generation bricks are formed, so that it becomes more truely 3D than most other variations seen on the web. These generally are 2D versions with rectangles replaced by bricks.

Photo


13 plus ones

14-May-16

A hinged tesselation made of hinged tesselations.

This one has 2 independent degrees of freedom, that are cycled in a 2:3 ratio. A lot of variations are possible. You can generalise to multiple levels. Each level can expand a factor of sqr(2), so with an infinite number of levels, you have an infinite expansion capability. Think of Sierpinsky structures that are hinged.

Animated Photo


14 plus ones

31-Mar-16
When I saw David Epsteins's post on Andrew Lipson's lego version over Escher's relatiivity (https://plus.google.com/100003628603413742554/posts/iAnkw9Dc1Bs), my thoughts went to this cardboard model I made a couple of years ago. I tried to sell it as a kit to the Escher foundation, but they don't seem to care much. Pity, it would be really nice, especially if printed on carboard, perhaps machine cut. So I thought I might as well post it on Google plus.

Photo


5 plus ones

19-Mar-16
The Postman cheered me up today: Laser cut plywood. I made a vectorisation routine, so I can laser cut conformal checkerboard patterns. I also converted a photograph of myself to a lasercut, tomorrow I will figure out how to assembel the pieces into some artwork.

Photo


3 plus ones

12-Feb-16

Reuleaux triangles

These are Reuleaux triangles. They have the special property of keeping constant width as they are rotated. That means they could be used as non-spherical ball bearings. A more usefull application is in the Wankel engine. I am actually working on compressors right now, some compressors lead to interesting maths.

Animated Photo

Comments:
Francis Siefken: That's pretty counter-intuitive, yes I've seen it before, but it's still amazing to see it having a constant width
10 plus ones

26-Jan-16

Warping Klein's quartic from 2D to 3D

I am planning to make an animation of the Klein quartic warping from a hyperbolic 14-gon to the 3D form. Just like Jos Leys already did, but I want to retain the individual triangles. (Jos uses a parameterisation which makes that difficult). I now have a 3D model and a 2D model, both with 336 triangles, but I need to map them to each other. To help visualise that, I made a paper model. I photographed it, because i am going to cut it up along the fundamental domain boundaries, and see how much it then folds out already to a 14-gon. In case you don't know what the hell I am talking about, here is the post by Jos: https://plus.google.com/108557640546882398221/posts/b9DGnAGJcwQ

Photo

Kris Ove: Yes! I also found the parameteristion that Jos Leys uses confusing, though the Klein quartic was beautiful. Hope you make progess with your animation. Gerard Westendorp: +Kris Ove

Its still on my agenda, I just had some other projects that took up my time!
16 plus ones

15-Dec-15

Retrograde uniform tiling

This is a *retrograde uniform tiling*. Uniform polyhedra can be non-convex, such as the great dodecahedron (https://en.wikipedia.org/wiki/Great_dodecahedron) , or the small inverted retrosnub icosicosidodehahedron. (https://en.wikipedia.org/wiki/Small_retrosnub_icosicosidodecahedron) The faces are allowed to intersect, as long as they are the same for each vertex, and all faces are regular polygons. Uniform /tessellations of the plane/ can be also kind of non-convex, but these are perhaps less well known. In fact I didn't know about them till last week, when I rediscovered them, and then saw them described as ‘retrograde tessellations’ on Wikipedia. But there are not so many nice pictures of them. One thing that makes them less pretty is that the faces ‘intersect’ in the same plane. So I curved them slightly, so it is clearer that these tessellations really are the equivalent of non-convex polyhedra, but on the plane. There are quite few of them, this is the fist one I could think of that might be nice. It consists of dodecagons and squares; de dodecagons intersect, and the squares ensure that each edge remains connected to 2 faces. So it is a bit like the Small rhombidodecahedron, (https://en.wikipedia.org/wiki/Small_rhombidodecahedron) replace the decagons by dodecagons. If you calculate the genus of this tiling, by expressing its Euler characteristic (Faces + Vertices – Edges) you find it is infinite. At each vertex, the sum of angles of the faces is greater than 360 degrees, so this is a kind of hyperbolic tiling, although it doesn’t look like one.

Photo

Comments:
James Buddenhagen: Help me out here a bit. It looks like the angles add to 360 at each vertex. What am I missing?
Gerard Westendorp: +James Buddenhagen
The tiling shares the same vertices with a tiling in which a hexagon, 2 squares, and 1 triangle meet, which add up to 360 degrees. But what the picture tries to convey, is that you have 2 dodecagons and a square meeting at each vertex, which add up to 150+150+90=390 degrees. The hexagons are supposed to be absent, I tried to make that clearer by curving the dodecagons, and leaving the hexagons as holes. (The triangle is also supposed to be absent) This is basically the same idea as for example with the great dodecahedron: You could see as a star with some dents in it, but it is supposed to be 12 intersecting penatgons. You need to train your brain a bit to see that.
17 plus ones

25-Nov-15

Folding a Klein Quartic

Jos Leys is making animations of polygons turning into hyperbolic surfaces: https://plus.google.com/108557640546882398221/posts/hdsvak2ZkYt He agrees it would be cool to do the Klein Quartic, but it is difficult...
I have a lot of old heptagon structures in my home, so I took one apart and converted it to a 14-gon, but instead of drawn on the Poincare disk, it is actually made of regular heptagons. The colors are the same as in the drawing on the right, which was by Tony Smith, and used on John Baez’s Klein Quartic page. On each vertex where 3 heptagons meet, the surface is not flat, the total angle is 360 degrees*(15/14). But if you fold the paper through the vertex, the curvature gets tidy, you can make a kind of flower. You could continue folding like that through the entire hyperbolic plane, I tried (perhaps succeeded, but I can’t prove it) to make an isometric C1 embedding of the hyperbolic plane: http://westy31.nl/Geometry/Geometry.html#Embed OK, so next we can try to connect the 14 sides of the ‘fundamental polygon’. I will try it tomorrow, but things might get horribly crumpled, to I thought I post this first, while it still looks relatively nice.

Photo


15 plus ones

29-Nov-15
In my previous post (https://plus.google.com/100749485701818304238/posts/R3wRrJYabtC), I made a fundamental polygon of the Klein Quartic out of regular heptagons. I wrote I would try and glue the outer sides together. Well, there is actually a way to glue the edges in the *wrong* way: If you look at the photograph, I have the 14-gon zig-zag folded into 14 identical (up to a reflection) triangles. Now I could glue the remaining edges together in the order of the ‘stack’, and loop the last one back to the first, this is just how the other 2 edges of the triangles already are glued. The resulting figure would be quite symmetric. I should be of genus 3, but I don’t see the 3 holes… The real Klein Quartic has the difficulty that the edges that need to be glued together are not adjacent in the ‘stack’. So after you glue a few edges, the others will be trapped.

Photo


8 plus ones

18-Nov-15

Logarithm of the Riemann Zeta function

This time, I made a conformal checkerboard animation of the *logarithm* of the Riemann Zeta function.
The complex log function is not single-valued. The imaginary part is the phase of (z), but you can always add a muliple of 2 pi to that. This causes our checkerboard pattern to be discontinuous along certain lines.
By taking the log of zeta, the zero's become poles (although they lie on the discontinuities, so maybe this has some issues...) We get new zero's, on those places where Riemann zeta was 1, since log(1)=0.
It looks pretty, and strange, but I don't know if it has any use.

Animated Photo

Frans Aris: alles op n=1/2 0? zoiets kon je toch een miljoen mee verdienen Gerard Westendorp: +Frans Aris
Zoiets ja. Die punten met oneindig veel vierkantjes zijn de 'nulpunten', die liggen volgens Riemann op 2 lijnen.
9 plus ones

14-Nov-15
The postman just brought stuff from the lasercut shop.

Photo

Comments:
Roice Nelson: So cool! What shop did you use? It looks like they can do quite large cutting areas. Gerard Westendorp: +Roice Nelson
Thanks! They are called snijlab: https://www.snijlab.nl/en The maximum dimension is 1200X600 mm. If you google online lasercutting, there is probably some shop more local. I love the 'living hinges', I want to make things with that.
13 plus ones

13-Nov-15
I have a new way of coloring complex functions: Using a conformal checkerboard. Complex functions are just like electric fields, the field lines run from north pole to south pole, which corresponds in the complex function to log(magnitute)=inf, and log(magnitude)=-inf. The electric field lines correpsond to lines of constant phase. (see http://westy31.nl/Geometry/Geometry.html#PhaseFlowPlots). So I thought, what if the lines of constant magnitude and lines of constant phase are at the same distance? You get conformal squares, which are squares that have 90 degree angles, but deformed sides. To turn it into an animation, I vary the criterion for the checkerboard color per snapshot. The idea for black and white conformal square pattern I got from David Gu's web site: http://www3.cs.stonybrook.edu/~gu/

Animated Photo


7 comments
Refurio Anachro:
:-p
Driss Moukaouame:
Merci pour ce travail bien documenté. C'est super....
Arthur Lawrence:
Great works-I do similar stuff with complex numbers and conformal images ~
15 plus ones

12-Sep-15
I now understand the #Leech lattice a lot better, I updated the section on my page: http://westy31.nl/Golay/GolayCodeAndSymmetry.html#Leech The picture is taken from Wikipedia, and colored to help interpret it. The vectors are arranged so the upper right triangle of the matrix is zero. This ensures that each new row is linearly independent of the previous ones, since it is the first to use a new column. The first (blue) row is a translation by 8. All translations by multiples of 8 are allowed, others can be made by linear combinations. The red rows are 11 legal Golay words multiplied by 2, which together with row 1 (the zero word mod 8) generate all Golay words multiplied by 2. The black vectors are translations by 4 in 2 different directions. Finally, the bottom green vector jumps from the even points to the odd points, while changing one coordinate by by an extra 4.
All these translations have squared length of at least 32.

Photo


5 comments
John Baez:
Yes, at some point some of us here on G+ had an argument about whether that normalization factor was biased toward 24 dimensions.
There's also another concept of density, the center density, i.e. one over the volume per lattice point. This is 1 for any unimodular lattice, I guess.
Gerard Westendorp:
+John Baez
I had not really thought about that, I just saw a graph of density versus dimension, eg on this page http:
//math.ucr.edu/home/baez/diary/november_2014.html with a sharp peak near the Leech lattice. The orignal graph is I think from Conway and Sloane. The density they plot is the çentre density', but they add a parabolic term to it which happens to be zero at N=24. I should mention that it has not been proven that the Leech lattice isthe densest packing, but there seems to be a pretty sharp upper bound on any improvement.
John Baez:
It seems pretty problematic to compare densities of lattices in different dimensions, but maybe there's some justification for that particular picture. The most interesting thing about it to me is that it has peaks at multiples of 8, which are related to Bott periodicity in a way I don't fully understand.
6 plus ones

08-Sep-15

Fermat's last theorem and powers mod N.

 I' ve been doing a lot of mathematics lately, and some old memories came up. When I was a student, I worked for a while on trying to prove #Fermat 's last theorem. I even believed I succeeded for about 3 days, until I found the mistake. One technique I used was to make tables modulo N, of powers of numbers. They give quite interesting patterns, and actually do give the integers quite a hard time satisfying a^n + b^n =c^n. For example, the picture is a table of the integers modulo 24, each row a consecutive power. Remarkably, the pattern becomes periodic after n = 3, all even powers >2 have the same residues mod 24, as do all odd numbers. Many combinations for a counter example of Fermat are forbidden modulo 24, as you can see from the table. But also modulo may other numbers put severe restrictios on the integers. Take for example modulo 7, as below: 1 2 3 4 5 6 7 1 4 2 2 4 1 0 1 1 6 1 6 6 0 1 2 4 4 2 1 0 1 4 5 2 3 6 0 1 1 1 1 1 1 0 1 2 3 4 5 6 0 Note for example the 6th powers, these are all 1. So the only way a Fermat counter example can exist for n=6 (or 12,18,24,…) is if one of the numbers is divisible by 7. Similar restrictions arise for a lot of other numbers. I find it quite addictive to stare at these tables. Once every while, you suddenly think, “Hey, but wait!, I see a proof of FLT…” Maybe I have to try modulo some monstrous moonshine numbers, I mean these haver periodicities that are deeply hidden in the modular tiling. Respect for Wiles and Taylor.

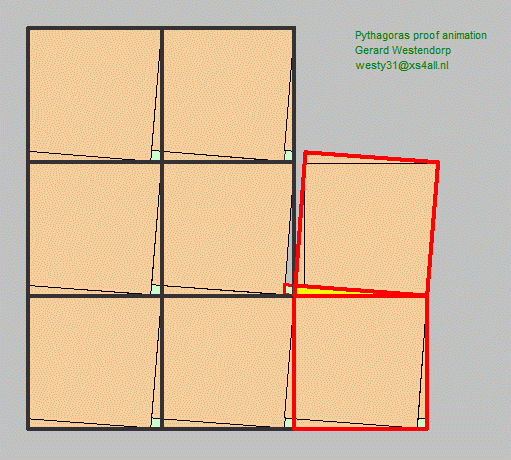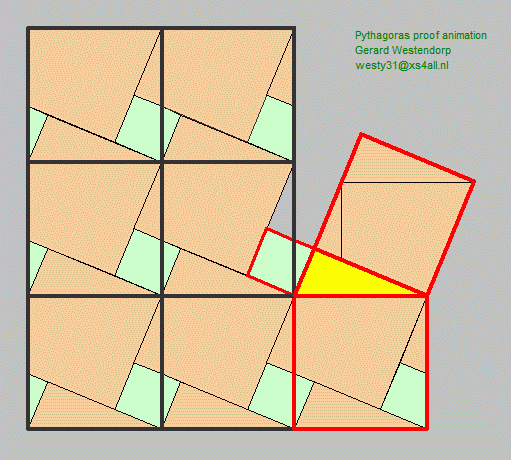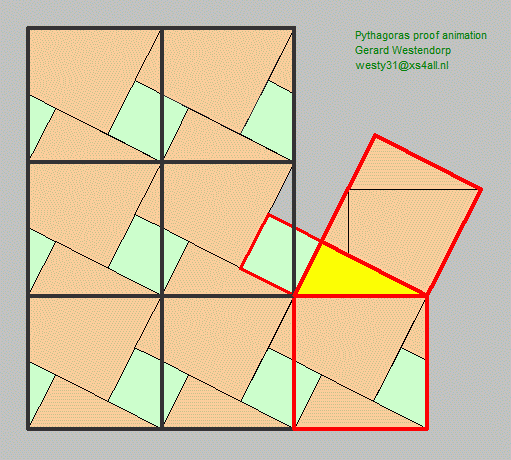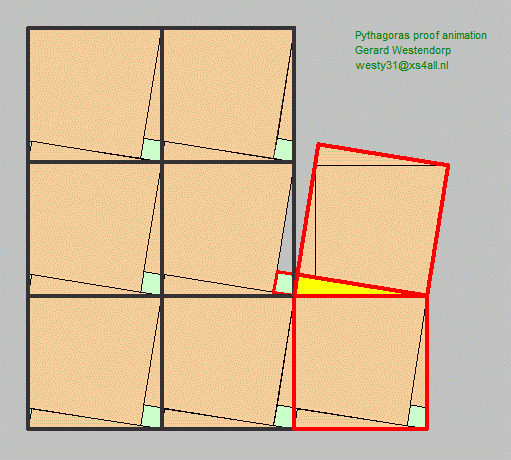
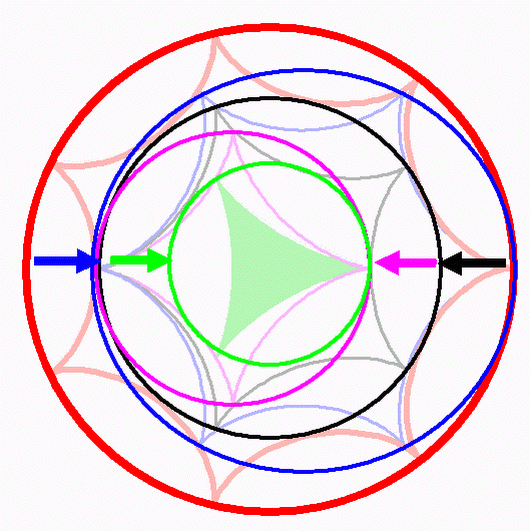
Photo


9 comments
Gerard Westendorp:+J Gregory Moxness
Did you look at Pascal's *pyramid*, a generalisation to higher dimensions?
J Gregory Moxness:
No, but I will - thanks.
Ion Murgu:
Fermat last theorem was solved , we need to make next steps.
5 plus ones

05-Sep-15

*Smart vertex labelling*

We have used our hands to count from 1 to 10 probably for thousands of years. Some people have remarked that it is a pity we do not have 12 fingers, because our number system would then have been nicer. (It only seems more involved to us because we are so used to 10-based numbers) The labelling of my fingers in the photo may seem a little weird. But if someone gave you a number “It is 3 mod 5, and 1 mod 2”, you could use it to find the number. The hand gives you the number mod 2 (left=0, right = 1), and the finger ordinal gives you the number mod 5 (thumb=0, little finger =4). I was surprised to find that a specification “a number is a mod p, b mod q, c mod r,…) uniquely gives you a number between 0 and ((p*q*r*…)-1 ). The proof is easy, once you see [The numbers p,q,r,.. need to be relatively prime] So for example a number between 0 and 5718 could be specified uniquely by saying “it is 21 mod 43, and 2 mod 19 and 5 mod 7”. How did I end up in this avenue of thought space? Well, I was getting increasingly irritated by constructing 3D images of polyhedra given its vertices. The problem is, you have to define all faces by specifying its vertices. For example, in the case of a dodecahedron, you have vertices 1-12, and a face is a pentagon labelled by its vertices, say 11,6,3,1,8. The way I used to do this is draw the dodecahedron, label it by hand, and then carefully look. Almost always, I made several mistakes. But polyhedra are deeply symmetric; surely this should not be necessary? The problem is to label the vertices in such a way that you immediately see its relation to its neighbours. For a cube, there is one nice way to do it: Label the vertices 0-7, so that the 3 binary bits of the number (0-7) are just the coordinates (x,y,z). So vertex 5 is binary 011, giving x=0,y=1,z=1, depending of course in which direction you read the bits relative to the dimensions (x,y,z). From this it is much easier to construct the edges and faces. So I thought, can you do something like that for the dodecahedron? Its 12 vertices are the 3 cyclic permutations of the set of 4 points (0,+-1, +-phi). phi is the golden ratio. Well, you could take the label (0 to 11) mod 3 to get the cycle count, and get the 2 sign bits for by taking the label mod 4. This is how I ended up thinking about these strange counting schemes. Actually, there is a more practical though not necessarily more interesting way of labelling that still allows the retrieval of information like above. Again using a,b,c..p.q,r,.., label it as a+b*q+c*p*q+…. This is just how our present number system works, using p=10, q=100, r=1000,.. Using “smart labelling” is related to the “Miracle Octad Generator” (MOG), that is used to describe symmetry group M24, Golay codes, and the Leech lattice. Things I have been pretty busy with these last days. Tiring but really cool!

Photo


4 comments
Layra Idarani:
The Chinese remainder theorem is so useful in modular arithemetic and finite abelian group theory, since it lets you paste things together from different prime moduli. Gerard Westendorp:
+Layra Idarani
I did not know the Chinese remainder theorem! It has been around for almost 2000 years.
Gerard Westendorp:
Just to mention an application, I can now for example more easily figure out the faces of an icosahedron. From the way I now label the vertex, I can figure out the coordinates. The 5 neighbours of a vertex, say (0,phi,-1):
( 0, phi, 1) (flip 1) // vertex number = 0*3+1=1
( phi, 1, 0) (left rotate) ) // vertex number = 0*3+0=0
( 1, 0, -phi) (right rotate&flip) ) // vertex number = 1*3+2=5
(-1, 0, -phi) (right rotate) ) // vertex number = 3*3+2=11
(-phi, 1, 0) (left rotate&flip) ) // vertex number = 2*3+0=6
For vertex numbering I use the position of the phi (0 to 2) + 3 times the binary code formed by the signs of the phi and the 1.
The rules for the 5 neighbours are:
1. You can rotate left, and rotate right, but if a phi and a 1 of 2 neighbours are in the same coordinate, they must be of the same sign, so their squared difference is always (1-phi)^2. 2. you can also flip, but only the coordinate who is 0 in the neighbour. Due to the fact that the golden ratio satisfies phi^2 = phi+1, all squared distances to neighbours are 4, as is required.
one plus one

01-Sep-15

Golay codes and symmetry

I figured out a way to understand Golay codes, and their relation to the Leech lattice, M24, and the Klein Quartic. I just completed this website: http://westy31.nl/Golay/GolayCodeAndSymmetry.html Golay codes are used in space communication to as a way to send data with built-in error correction. You can construct the Golay code by imagining 12 data bits on the respective 12 pentagonal faces of the great dodecahedron. Then on each of the 12 vertices, put a parity bit that is the parity sum over all face bits that are *not* connected to the vertex. That's it! Note that there are 7 of these faces, and each of the 12 faces has 7 parity bits related to it, so there is th 24-7 connection to the Klein Quartic.

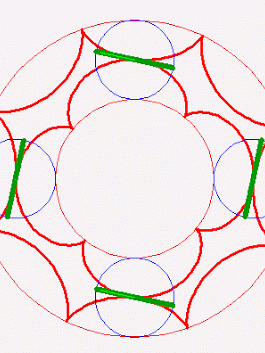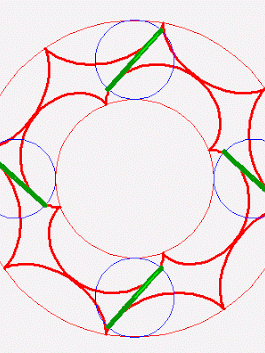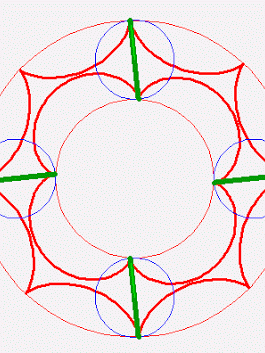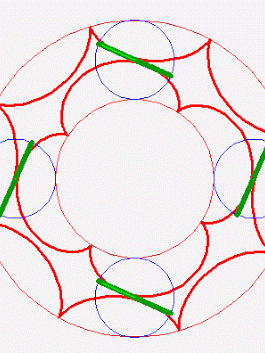
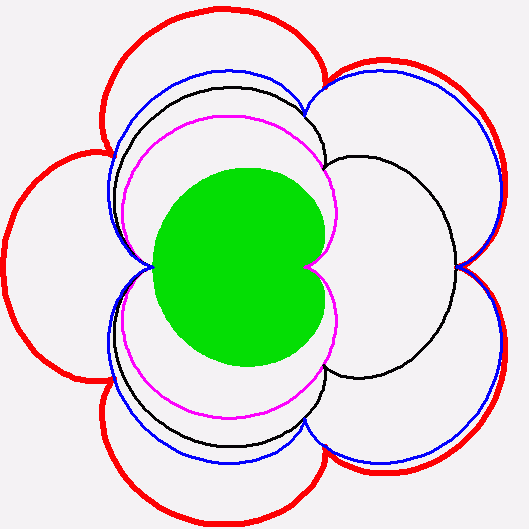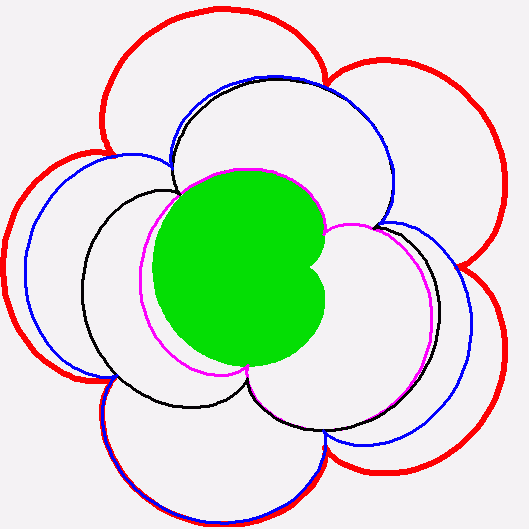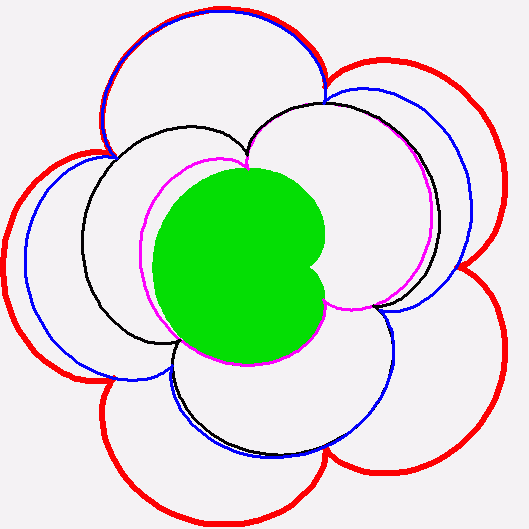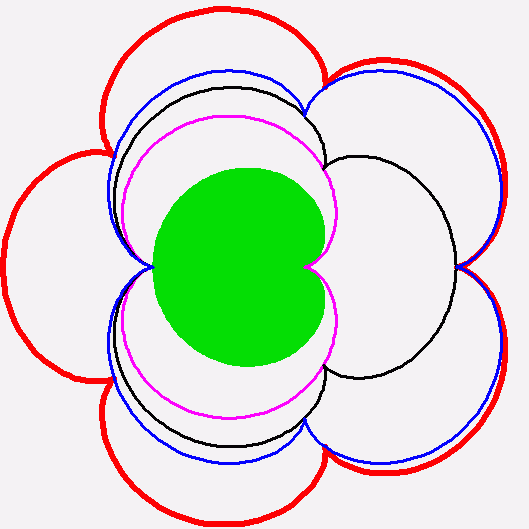
Animated Photo

25 comments
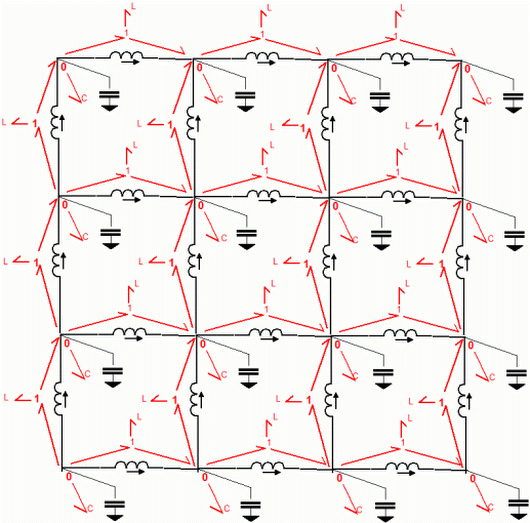
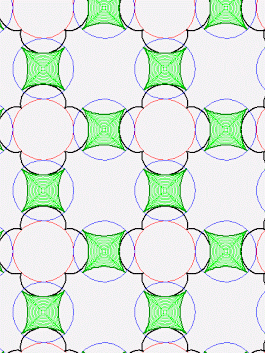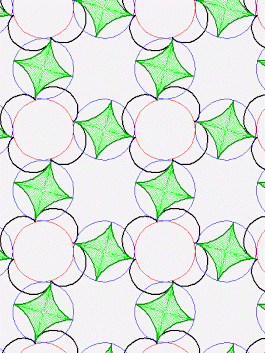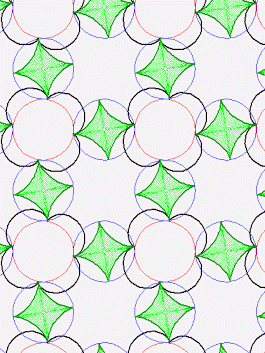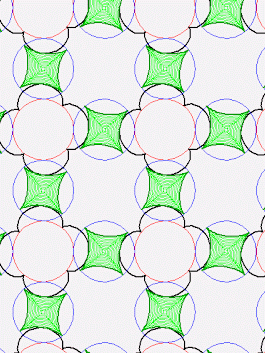
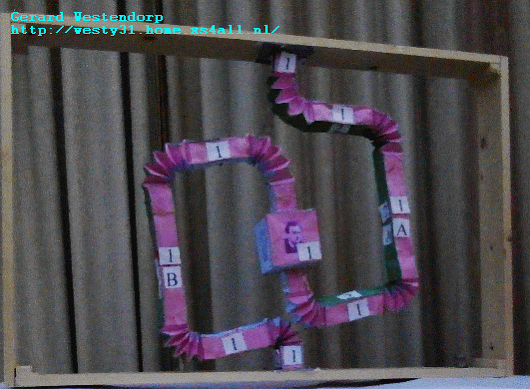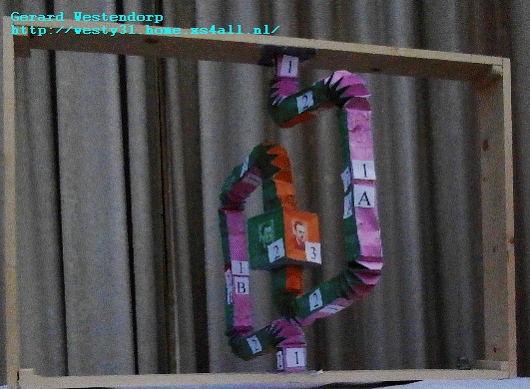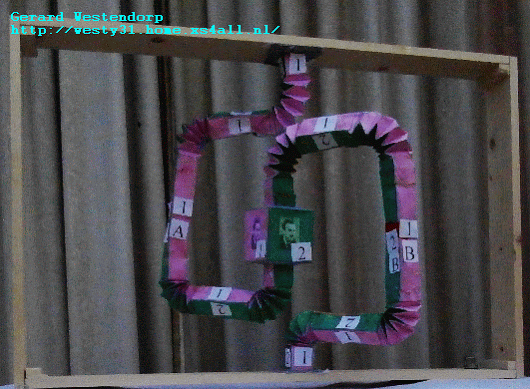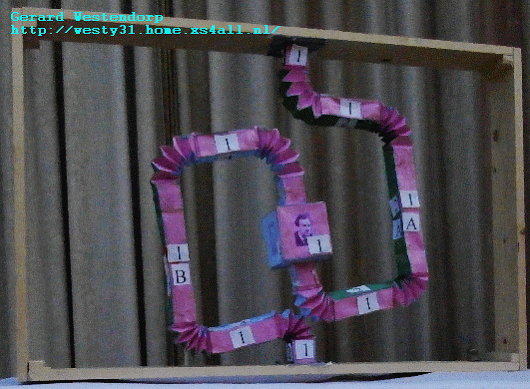John Baez:
This is great!  If you (or someone) could reduce the size of the gif to below 1 megabyte, I could, with your permission, feature this idea in my American Mathematical Society blog Visual Insight.
Otherwise I might just use an image of the great dodecahedron, or the generator matrix for the Golay code.  But the idea here is wonderful!
John Baez:
By the way, your web page on the Golay code is great, but it would look nicer if you put a line of space before and after each image, and centered them.  For example, this:
the Golay code, is related to the magical symmetry group M24.<br> <img style="width: 305px; height: 297px;" alt="Atlas of FInite Groups with 3D print of Great Dodecahedron" src="Atlas.jpg">My curiosity for M24 was sparked by remarks like this produces an image that's jammed up against the text in an uncomfortable way. 
This fixes that:
the Golay code, is related to the magical symmetry group M24.<p>
<div align = "center"> <img style="width: 305px; height: 297px;" alt="Atlas of FInite Groups with 3D print of Great Dodecahedron" src="Atlas.jpg"></div>
<p>My curiosity for M24 was sparked by remarks like this
John Baez:
Your page says
"Let us now define the Leech lattice in a way we can understand."
But you do not, in fact, define it.  Are you planning to do so?  As far as I can tell, the Leech lattice is to the integers as the Golay code is to the integers mod 2.
John Baez:
Your page also says:
"All finite groups have now been classified."
This is not true.  Only the finite simple groups have been classified.  From these we can build up all finite groups by iterated "extensions".  However, this can be done in so many ways that it's generally considered impossible to classify finite groups.
Refurio Anachro's profile photo
Refurio Anachro:
> you do not [...] define the [Leech lattice]
Maybe he edited it, but i just read:
>> In 24 dimensional space, [...] consider all points with integer coordinates. [...] keep only those points whose coordinates modulo 2 are legal Golay codes. That is the Leech lattice!
Isn't that enough, +John Baez​​?
Refurio Anachro:
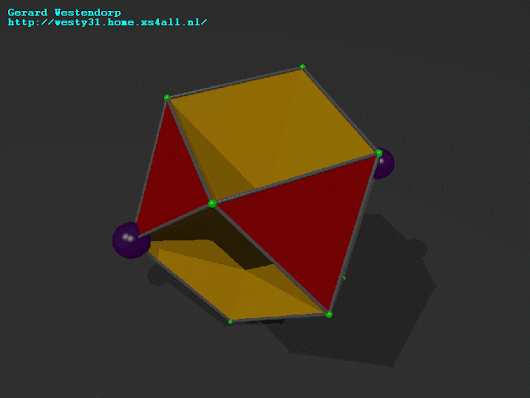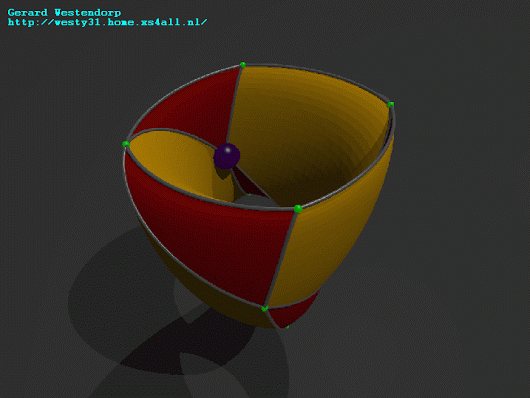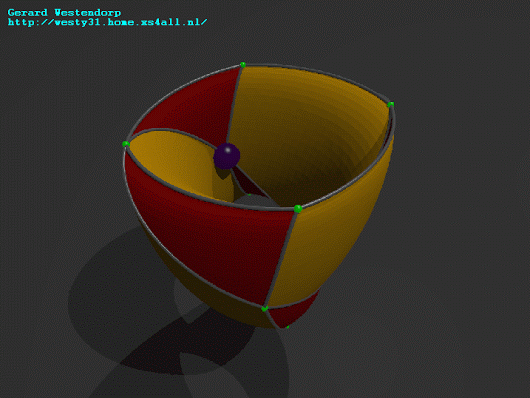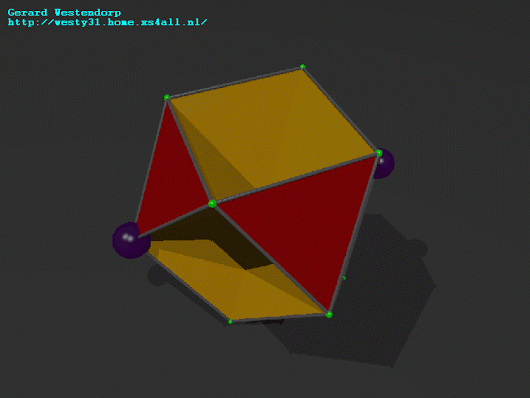
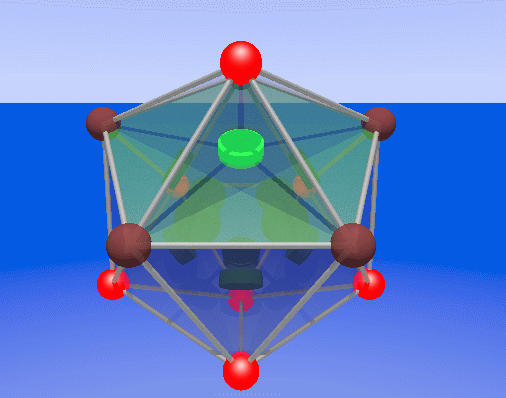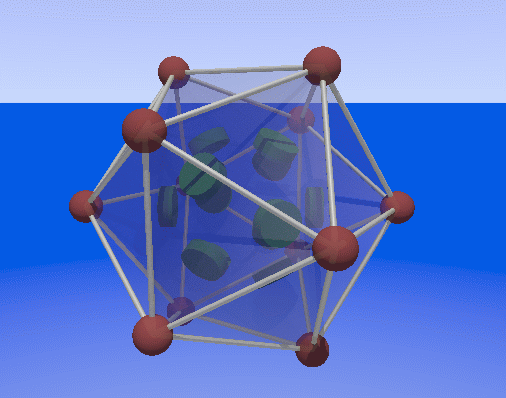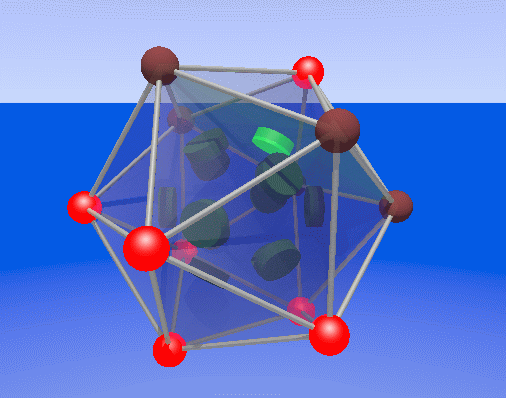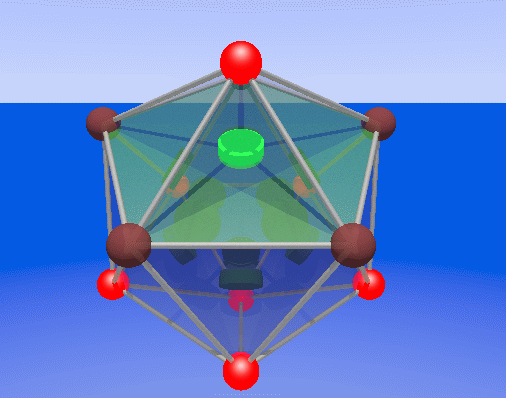
Great post +Gerard Westendorp​​! The small stellated dodecahedron is the dual of the great dodecahedron. That means either one's data is the other's parity, right?
I hope i can find the time to enjoy the references later today, and maybe write a bit. Fun fun :)
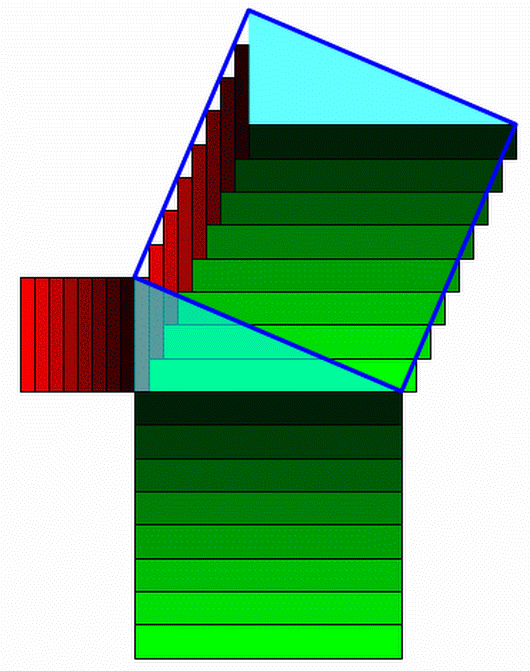
Gerard Westendorp:
+Refurio Anachro Thanks! I've updated the website, mentioning the fact that the 2 polyhedra are dual.
Gerard Westendorp:
+John Baez
Thanks! I've put a 0.98 MB version, against a black background, on the website. (It's all free to copy) Also I centred the images, as you sugested. (I have an outdated HTML editor). And thanks for the comment on simple groups versus general groups, I corrected it.
Gerard Westendorp:
+John Baez As for the Leech lattice, my description is/was not correct.
I have an article on the Leech lattice, which I use to try and get a correct definition, which will hopefully appear before I fall asleep. Basically, I said that you do the integers modulo 2, and then check if they are Golay words. But that would imply that translation vectors like (1,0,0...) can be applied to Leech lattice points, which is not true. The proper definition involves a more complicated condition of integers modulo 2,4 and 8, that I will try to get right.
Refurio Anachro:
Nice +Gerard Westendorp​. I should have looked up that definition for the Leech lattice earlier! Wikipedia has it a bit terse. I'd guess there are two types of vectors, some with mod 8 in their construction, and some with mod 4.
And that rings a bell... AFAIR, John recently posted a thread leading to a detailed derivation of these vectors, was it on the cafe? Not sure what the approach was though.
John Baez:
+Gerard Westendorp - thanks for making that smaller image!  Unfortunately I think it's too unpretty for Visual Insight, because there's a lot of aliasing (or something) occuring on the dodecahedron edges - you can see strange lines on them.  An image that didn't rotate could be much smaller while still being beautiful.  Or maybe someone who is good at writing efficient gifs could help - Greg Egan took a 2.5 Mb gif someone else made and used a program of his to compress it to < 1 Mb.
John Baez:
+Refurio Anachro wrote: "Isn't that enough, John Baez?"
Yes, that would be enough, somehow I didn't see that.  Maybe it's not true.  But I don't understand Gerard's argument:
+Gerard Westendorp wrote: "Basically, I said that you do the integers modulo 2, anf then check if they are Golay words. But that would imply that translation vectors like (1,0,0...) can be applied to Leech lattice points, which is not true."
No, that translation would change the parity.  You can only do translations like (1,1,0,0,...) and (1,-1,0,...) (with all possible permutations of coordinates, and of course sums and differences of such translations).  Does that help?
John Baez
+Refurio Anachro wrote: "AFAIR, John recently posted a thread leading to a detailed derivation of these vectors, was it on the cafe? Not sure what the approach was though."
Yes, Greg Egan and I studied the "Turyn construction" of the Leech lattice, here:
http://math.ucr.edu/home/baez/octonions/integers/integers_9.html
This finds the Leech lattice inside the direct sum of 3 copies of the E8 lattice.  This copies Turyn's 1968 construction of the Golay code starting from 3 copies of the 8-bit Hamming code.
None of this is as simple as I'd like - I'd love to see a 'great dodecahedron' approach to the Leech lattice!  One advantage of connecting the Leech lattice to the E8 lattice is that it put the Leech lattice inside the 27-dimensional exceptional Jordan algebra in a nice way.  We discuss this in the next page of this series:
http://math.ucr.edu/home/baez/octonions/integers/integers_10.html
I want to publish a paper based on that, because it winds up involving some rather beautiful and deep mathematics.
Gerard Westendorp:
+John Baez
About making a prettier and smaller animation: That might well be possible, my GIF animator is a little program called "Unfreeze", which is very minimalistic.
Prettyness pays off I think, I would not mind spending more time on it, if it makes nicer pictures. (I like the ones by Klein and Fricke, which had to be wood-carved, so that they could be printed in 19th century presses.)
John Baez:
+Gerard Westendorp - your construction of the Golay code is a beautifully geometrical way of understanding this terse statement on Wikipedia:
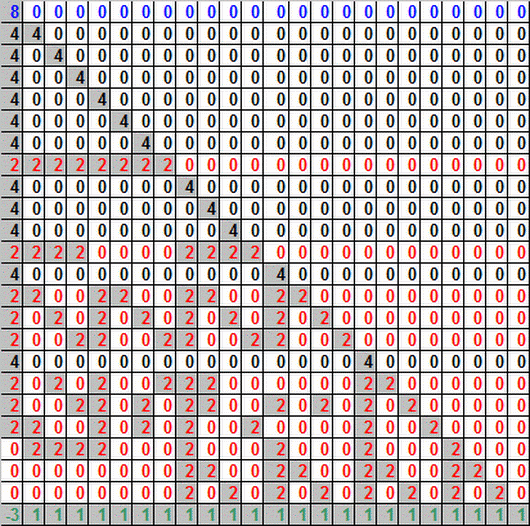
"A generator matrix for the binary Golay code is I A, where I is the 12×12 identity matrix, and A is the complement of the adjacency matrix of the icosahedron."

https://en.wikipedia.org/wiki/Binary_Golay_code#Constructions
There's no reference cited here, but it's probably in Sphere Packings, Lattices and Groups, and as you note it's in this page you cited:
http://giam.southernct.edu/DecodingGolay/encoding.html
Refurio Anachro:
Try gifsicle, a commandline knobset just for what gif has to offer.
Refurio Anachro:
I thought I did understand Gerards argument, but I can't make it cohere with this:
https://en.m.wikipedia.org/wiki/Leech_lattice
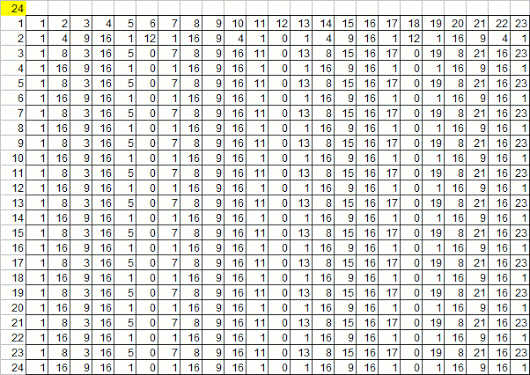
The Leech lattice can be explicitly constructed as the set of vectors of the form 2^−3/2 (a1, a2, ..., a24) where the a_i are integers such that
a_1 + a_2 + ... + a_24 ≈ 4a_1 ≈ 4a_2 ≈ ... ≈ 4a_24 (mod 8)
and for each fixed residue class modulo 4, the 24 bit word, whose 1's correspond to the coordinates i such that a_i belongs to this residue class, is a word in the binary Golay code.
Edit: Yours looks like a better pick, John. I'll have to try again then.
John Baez:
+Refurio Anachro wrote: "where the ai are integers such that
and for each fixed residue class modulo 4..."
That looks like either it's missing an extra clause or has an unnecessary "and".  It would be very nice if there weren't an extra clause!
John Baez
There's an extra clause: the sum of all the a_i equals each one of the numbers 4a_i mod 8.
Refurio Anachro:
+John Baez​ like so:
> There's an extra clause
Right. I just filled the blank i had pasted. Thanks!
> It would be very nice if there weren't an extra clause.:-)
It has been such a nice hike so far that i'm not ready to give up on that undreamt prospect to get to see the Leech lattice by foot. I'll shoot my arrows to the sky, if necessary.
Now where did i put that book of Conway...
Refurio Anachro:
I'm looking at Conway and Sloane's "sphere packings, lattices and groups", and here's the first excerpt that might help shedding light on the issue. It's just the first I got to, if Gerard is ok with this I'd add some more later.
In the preface to the third edition they write about the Leech lattice:
> Lift the binary Golay code to Z4 [...], and apply "Construction A4"
> the cyclic code with the generator polynomial g2(x) = x^11 + x^9 + x^7 + x^6 + x^5 + 2x^4 + x - 1, a divisor of x^23 - 1 (mod 4). By Hensel-lifting this polynomial (using say Graeffe's root-squaring method) to Z4 we obtain
> g4(x) = x^11 + 2x^10 - x^9 - x^7 - x^6 - x^5 +2x^4 + x - 1
> a divisor of x^23 - 1 (mod 4). By appending a zero-sum check symbol to the cyclic code generated by g4(x) we obtain a self-dual code of length 24 over Z4. Applying Construction A4 (cf Chapter 5), that is, taking all vectors in Z^24 which when read mod4 are in the code, we obtain the Leech lattice.
> In this version of the Leech lattice the 196560 minimal vectors appear as 4.16.759 of shape 2^2 1^8 0^14, 2.24.2576 od shape 2^1 1^12 0^11 32.795 of shape 1^16 0^8 and 48 of shape 4^1 0^23.
Gerard Westendorp
+John Baez
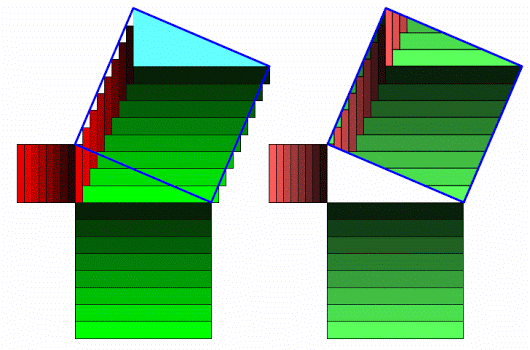
 I made a new try for a smaller image, it is only 230 kB, not moving. It is adjacent to the old one on the web page.
Gerard Westendorp:
It is getting late, but I am drawing a hyperbolic polygon on a (7,4) tiling, with the connectivity of the Golay matrix. It has 24 heptagons. I think it has 84 edges, like the Klein quartic, but only 42 vertices, it has genus 10. (Hopefully this is not complete nonsense, I will check tomorrow)
John Baez:
+Gerard Westendorp - thanks, that's nice! Greg Egan also made one, that's a bit different. I'll use both on my /Visual Insight/ article, and of course credit both of you - and especially /you/, for having this nice idea.
Gerard Westendorp:
I fixed the part on the Leech lattice, I think I now understand it:http://westy31.nl/Golay/GolayCodeAndSymmetry.html#Leech
I also read that Leech himself didn't get it right the first time, comforting thought.
15 plus ones

24-Aug-15
OK, one more...

Animated Photo


Comments:
 John Baez: Nice! I took the liberty of posting this to /Azimuth/, here:
https://johncarlosbaez.wordpress.com/2013/12/03/rolling-hypocycloids/#comment-70136
8 plus ones

24-Aug-15
I have been in a couple of discussions before on rolling cycloids, that fit together exactly, I found a new cool variation: The innermost and outermost cycloid both stand still.

Animated Photo


4 comments
John Baez:
What's the trick that makes these work? I took the liberty of reposting this to /Azimuth/, where we have quite a gallery of rolling cycloids and hypocycloids:
https://johncarlosbaez.wordpress.com/2013/12/03/rolling-hypocycloids/#comment-70136
Gerard Westendorp:+John Baez
Thanks for putting it Azimuth, the place where the rolling hypocycloids I guess first appeared. I will try and write a post explaning the trick behind this.
John Baez:
Thanks! And it would be great if you post a comment on Azimuth with a link to your explanation.
11 plus ones

13-Jun-15
A laser cut Mandelbrot, by Jens Alfke. Laser-Cut Mandelbrot Set Laser-Cut Mandelbrot Set flickr.com
4 plus ones

17-May-15
Someone (I can't find the post, it is somewhere on google plus) mentioned it would be nice to add a letter 'd', occluded by the 'n', so that you get 'open/closed' instead of 'open/close'. That was easy to add, so I did it.
Apparently, the original gear wheel version of this is by Ikeda Yosuke: http://homeli.co.uk/open-close-clockwork-sign-by-ikeda-yosuke/

Animated Photo


2 plus ones

17-May-15
This "Perspectagram" implements an anagram by viewing the letters from 2 different view points (perspectives). If you think about it, you can see that you can implement an arbitrary anagram in this way: Put the letters on a grid, and let the grid coordinates (i,j) correspond to the 2 indices of the letter in the 2 phrases of the anagram. The grid is not orthogonal, but formed by lines emanating from the 2 viewpoints. This particlular anagram, "Metamagical Themas" <-> "Mathematical Games", was used by Douglas Hofstadter when he succeeded Martin Garnder as writer of the mathematical column in Scientific American.

Animated Photo


5 plus ones

01-May-15
In response to https://plus.google.com/100749485701818304238/posts/bpgtU3uu7qa, a gear wheel version of this, here is an "Open-close mechanagram" based on linkages. I might make a nice version of it later. It is easy to make, for example with card board, once you have the lengthes of the linkages.
I can think of a method for making an arbitrary mechanical anagram ("mechanagram"), similar to this one.

Animated Photo


3 plus ones
19-May-15

Voldemort "mechanagram"

This example illustrates a general method for implementing an arbirary "mechanagram", a mechanical realisation of an anagram. For the #HarryPotter fans, like myself. Another interesting way of implementing an anagram, which I thought of while making this one, is the "perspectagram": https://plus.google.com/100749485701818304238/posts/JT8hvcRaqkZ

Animated Photo

Comments:
Gerard Westendorp: For the original movie scene, go to 2:30 minutes: https://www.youtube.com/watch?v=B6NxD7RQPF0
8 plus ones

27-Apr-15
An old #invention of mine: A #pop-up that expands larger than the containing card. The construction becomes more rigid as it unfolds.

Animated Photo


2 plus ones

28-Mar-15

Bond graphs and circuit equivalents

I had some interesting discussions on Bond graphs last week. They are part of a "unified" modelling approach, just like my favorite approach: electric circuit analogy. Luckily, I found these are equivalent, so I do not have to completely reorganise my brain. Below is a picture of a 2D acoustic medium, modelled in black as circuit equivalent, and in red as Bond graph. More info at: http://westy31.nl/Electric.html#BondGraph

Photo


5 comments
John Baez:
+Gerard Westendorp - yes, I'm writing a paper about that category! I blogged about it a bunch on /Azimuth/, but the paper itself goes further:

http://math.ucr.edu/home/baez/circuits.pdf
It needs to be polished a bit more.
Gerard Westendorp:
+John Baez
Thanks, I'm taking a look at it, looks interesting. Do you, or perhaps one of your students, know if you can simulate an arbitrary Nth order linear differentail equation with an M-node circuit? As an extra freedom you would be allowed to measure voltage in different units in each node, and you are allowed to use negative values for R,L and C. I was trying to figure this out, but I thought perhaps it is part of standard literature.
Gerard Gerard Westendorp:
About simulaing an arbitrary N-th order differential equaiton, i just figured out a really cool answer to that. I will try to write that down tomorrow in a separate post!
2 plus ones

16-Nov-14

3D print of a Klein Quartic Fruit bowl

I made a 3D print of a Klein Quartic Fruit bowl. I think I'll also make a slichtly larger black version. Unfortunatly, the price of 3D printing scales with size. Royce Nelson also made a nice 3D print of Klein's Quartic. Here is the web shop page, in case you need a fruit bowl: http://www.shapeways.com/model/2818514/klein-quartic-fruit-bowl.html

Photo


6 plus ones

03-Oct-14
My latest 3D print, compound of 5 tetrahedra.

Photo


6 plus ones

09-Sep-14

Ising model

In this discussion: https://plus.google.com/117663015413546257905/posts/P2N72KWZtyZ, I mentioned a spreadsheet of the Ising model that I made. If you want to play with it: http://westy31.nl/ScrapBook/Ising.xls

Photo


no plus ones

07-Sep-14

Lecture on Turing

I was amazed by this lecture on Turing. There is some stuff declassified only in 2000, and therefor not in most history books. Aparently, the British had a 1 MHz computer in 1943, built with radio valves. (This was not the better known Bombe that cracked the Enigma, but a more advanced computer, years ahead of its time) EngineerTommy Flowers had built it in 10 months, without the support of the sceptical Brittish intelligence. He was not allowed to talk about it after the war. Turing used algorithms for decription that are advanced even today.

Photo

Turing: Pioneer of the Information Age
one plus one

05-Sep-14
Animation of epicycloid and hypocycloid gears tiling the plane.

Animated Photo Animated Photo





25-Aug-14
I got an old lamp from a second hand store, and rebuilt it to a stereographic projector for 3D printed polyhedra. The idea of using a LED light to imitate a stereographic projector I borrowed from Henri Segerman: https://plus.google.com/112844794913554774416/posts/MTJg2Y4Kmgt
To get a real sterogrpahic projection, you need a sphererical object, but I wanted to use my 3D prints in some way, they are now just lying around. So this lamp gives only approxmately stereographic projections. The 4 white LEDs are about 20 Candela, so 20X more light than a "standard candle". This was about the brightest I could get. To power the LEDs, I used an old phone charger. Connecting the LEDs directly worked, but I put in a resistor anyway to limit the current. I left 1 of the 5 old bulbs intact, so that I can also use the lamp in a practical way.

Photo Photo

Comments:
 Bruce Elliott: Very nice!! How long before these are available on etsy.com ? ;-)
Gerard Westendorp: +Bruce Elliott
Thanks, making replica's could be a good project. but I start new projects faster than I can complete them, so my succes rate is a highly chaotic funciton of time...
5 plus ones

27-Jun-14

Carpenter's Pythagoras proof

#geometry Inspired by a recent post on Google plus (https://plus.google.com/101584889282878921052/posts/Ld2X7WoSbCR), I came up with the "Carpenter's Pythagoras proof". Note the the staggered boards cover the same area as the boards aligned into 2 squares. But they also have the same area as the hypothenuse square, after cutting and pasting the cyan triangles.

Photo


no plus ones

28-Jun-14
#Geometry Carpenter's Pythagoras proof by a more diligent carpenter: Now all boards have been explicitly cut to fit into the hypothenuse square.

Photo


Comments:
 Richard Green: Nice! You have to think about it, but it's worth it.
3 plus ones

16-Jun-14
Nice light this evening; Good for some photographs of my 3D prints.

3 Photos - View album


3 plus ones

02-Jun-14
I started 3D printing! Check out my webshop under construction at: https://www.shapeways.com/designer/Gerard_Westendorp

Photo


3 plus ones

25-Apr-14
A new animation: A 5 hypocycloid rolling in a 4 epicycloid. Note all (inner and outer) cusps touch the other curve.
More discussion here: http://johncarlosbaez.wordpress.com/2013/12/03/rolling-hypocycloids

Animated Photo


3 plus ones