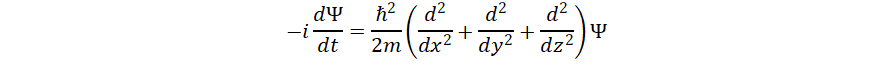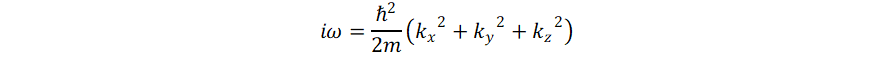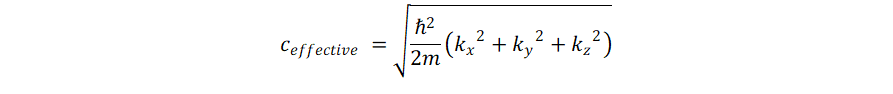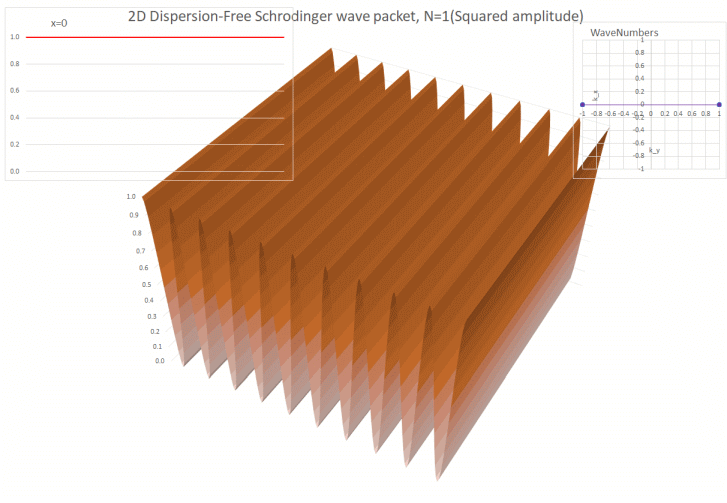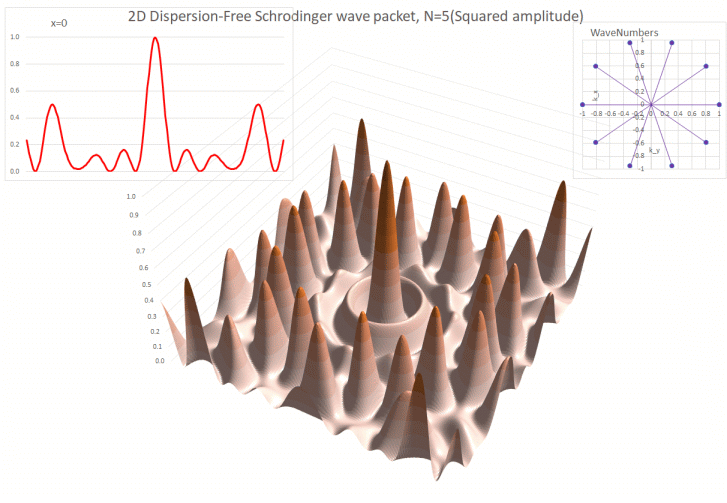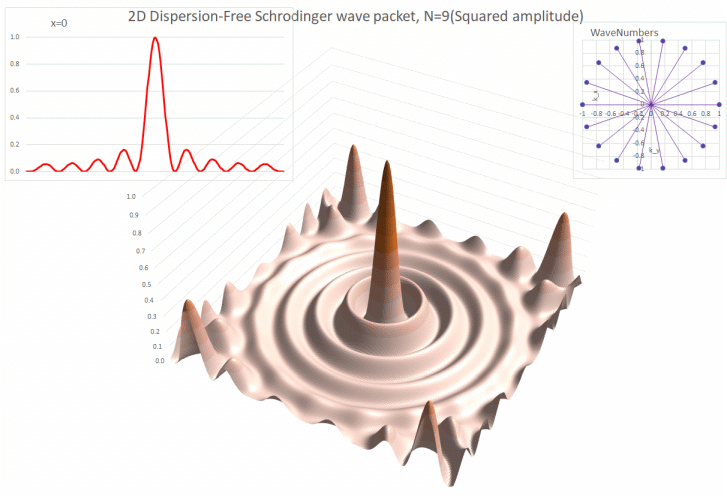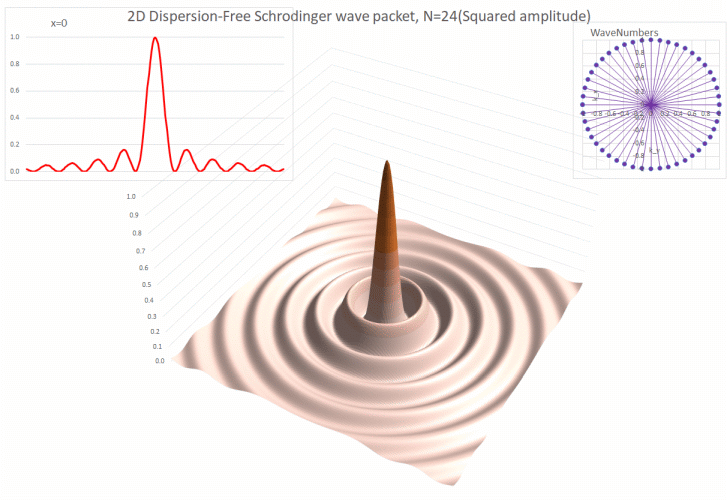
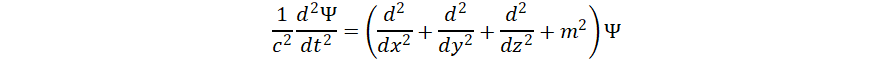
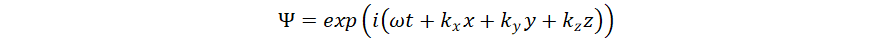
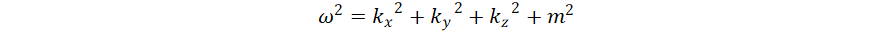
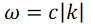 for no
dispersion. If the wave equation
describes a massless particle, then there is no dispersion. So the
Maxwell equations, which describe light, radio waves etc, have no
dispersion. Neither does sound in air. This makes these waves suitable
for communicating across distances. But try sending a message across a
lake using water waves...
for no
dispersion. If the wave equation
describes a massless particle, then there is no dispersion. So the
Maxwell equations, which describe light, radio waves etc, have no
dispersion. Neither does sound in air. This makes these waves suitable
for communicating across distances. But try sending a message across a
lake using water waves...