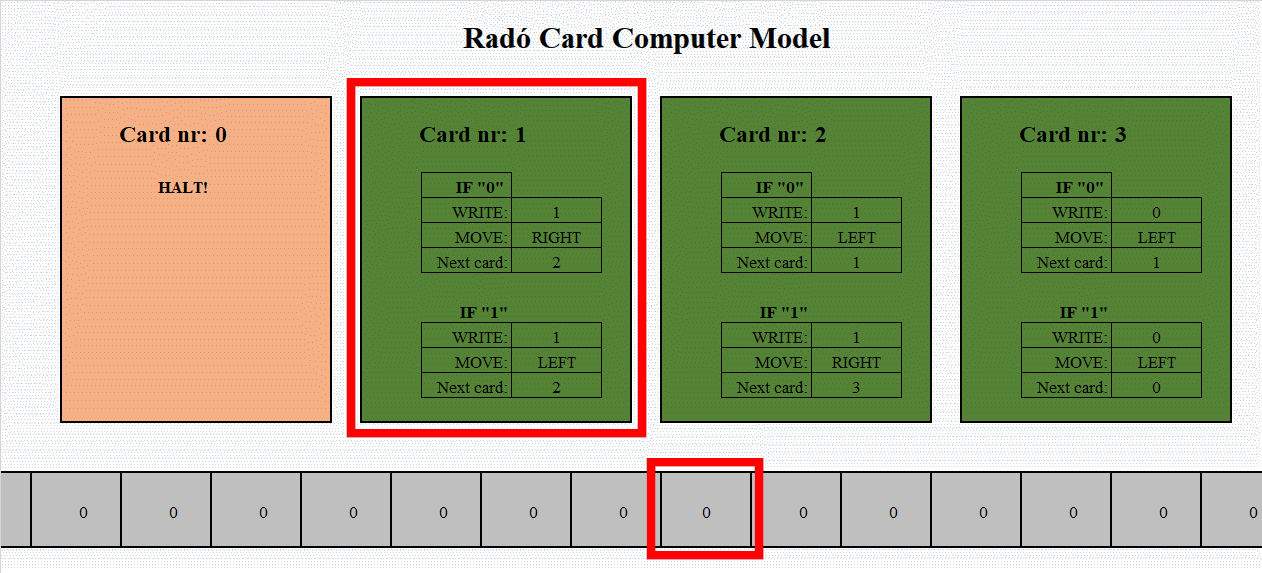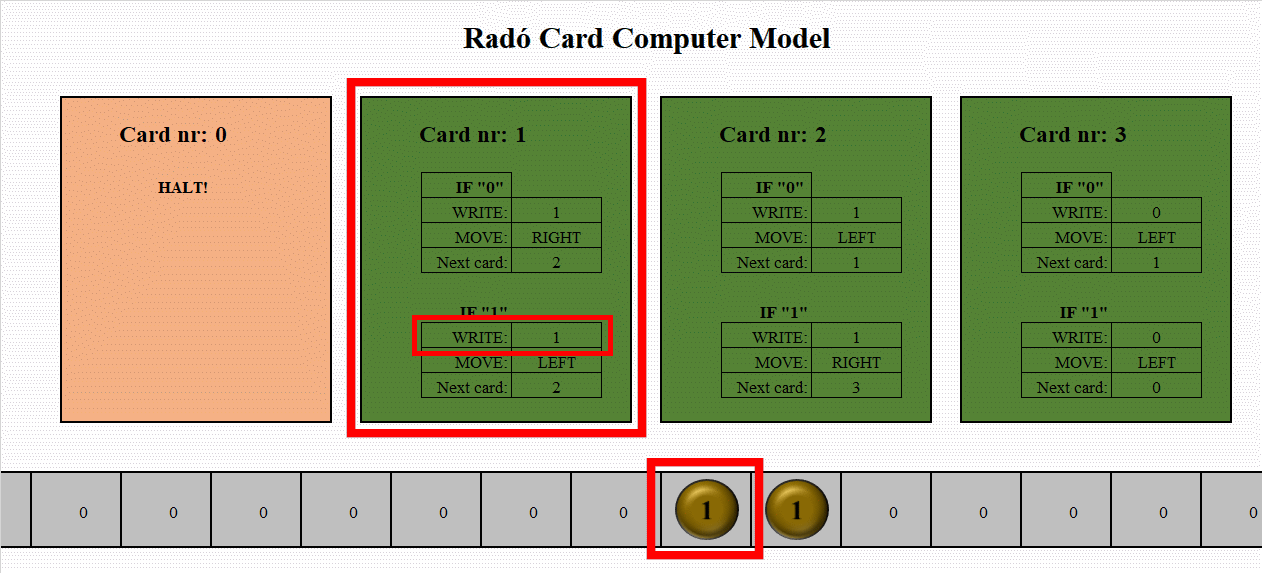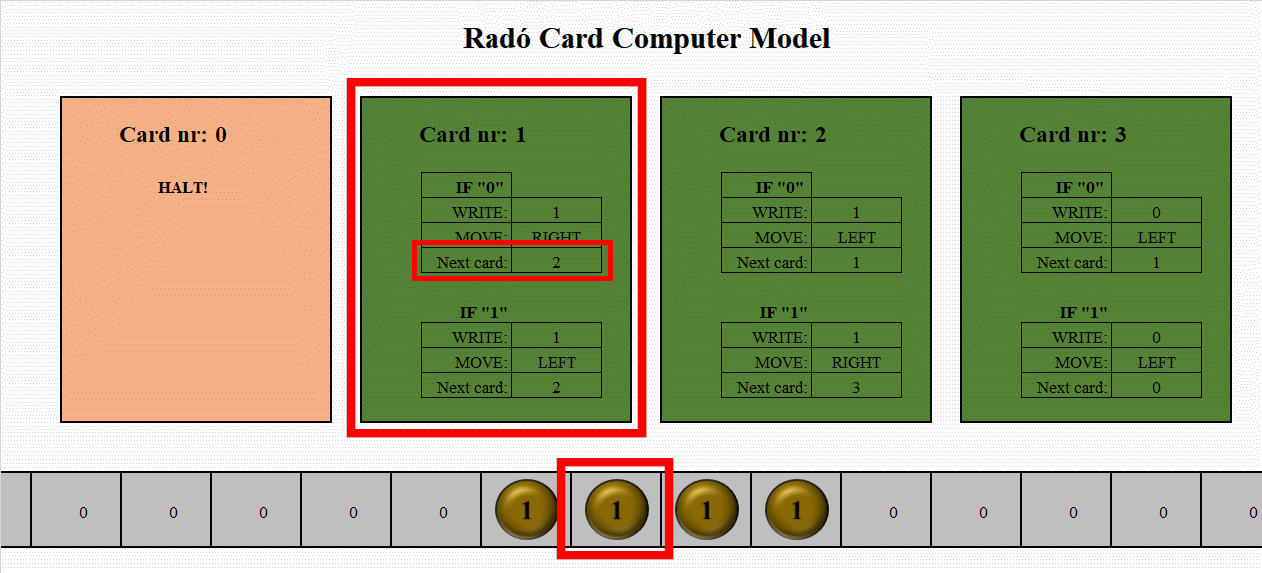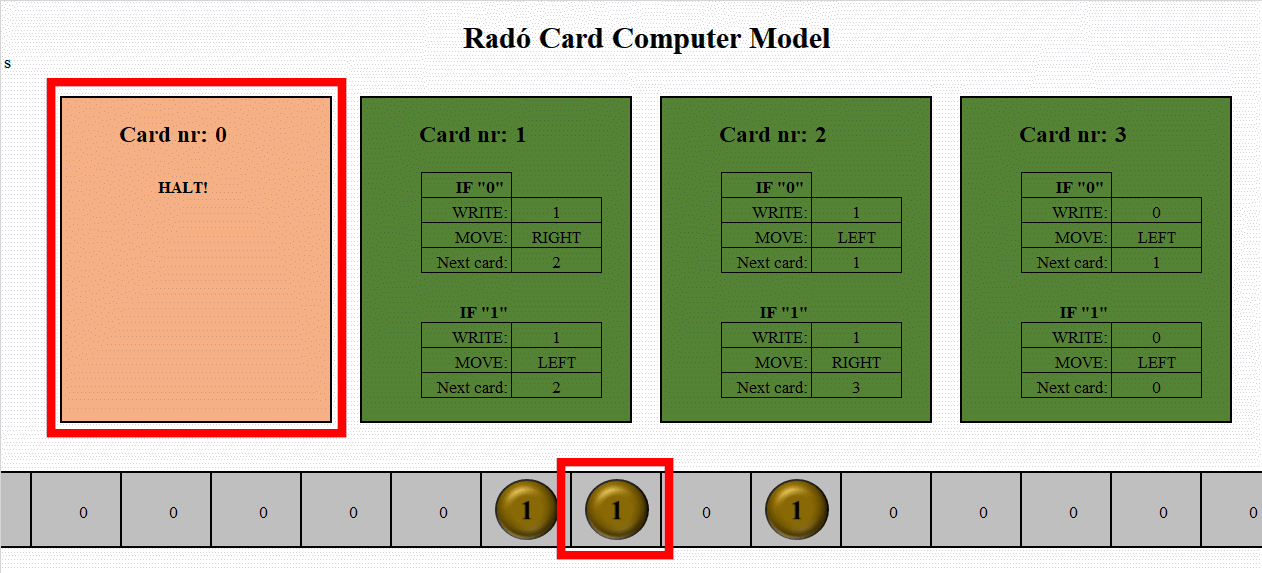
The Universal machine

Move Website

My website is moving. Best go to the new location at westy31.nl/UniversalMachine/TheUniversalMachine.html This old page will be gone soon...

Other stuff by me
This web page is about my favorite invention: The Universal machine.
The Universal machine aka the Computer, can in principle imitate all other computing machines. Not just all those that have ever been made, but any thinkable machine. Including our own brains. The one simple idea behind it has already had a huge impact on our civilization, and it will impact our future in unforeseeable ways. Also, the idea of the Universal machine is very important in philosophy and mathematics. Any thinkable thought can be thought by a computer, what is thinking?
So trying to understand this stuff might be a good idea.

Turing

Turing

Alan Turing (1912 -1954)

I am a bit of a Turing fan. Many see him as the cool but tragic guy that invented the computer. In 1936, he published a new way of solving Hilbert Entscheidungsproblem (I'll explain later), a few years after Gödel (1931) and Church. But Turning's proof is much easier to understand, and it explains the basic idea behind the computer, and how it is universal. In world war 2, he successfully worked on cracking the Nazi code "Enigma", making use of one of the the first computers. He died young, presumably by having eaten part of a poisoned apple. He was persecuted for being a homosexual.

Other people

Leibnitz

Gottfried Leibniz (1646 -1716).

He invented the binary system (1 and 0). He foresaw many of the idea’s the other people mentioned here. But he was very far ahead of his time… Luckily he also did a lot of other things that made him famous in in his own days. He is also well known for inventing calculus, at the same time and independently from Newton.

Babbage

Charles Babbage (1791-1871).

He built machines that could do calculations, and philosophized about this. Although Babage built working computing machines, he did not get to finish his "Analytical Machine", which might have been a universal machine.

Lovelace

Ada Lovelace (1815- 1852).

She wrote a computer program for calculating Bernoulli numbers, to be implemented on Babbage’s Analytical Machine. She did things almost no women did at the time.

Hilbert

David Hilbert (1862 -1943).

He was an influential mathematician, who wrote down Hilbert’s 23 problems, which continue to define mathematical research. Hilbert’s Entscheidungsproblem is not quite in this list of 23, although it is related to the 10th problem.

The Entscheidungsproblem is related to the idea that if you reduce a mathematical proof to its bare bones, you end up with using a small set of “logically allowed rules” to get from a “true statement” to another “true statement”. The whole proof can be broken down into a chains of these rule applications. If you follow the chains “upstream”, you end up at the “Axioms”. The axioms cannot be proven (or no one knows how). But there only a few of them, and they form the basis of a mathematical theory. Euclid (300 BC) showed how you could do geometry from just a few axioms. In the Greek days, an axiom was thought to be some kind of “god given truth”. But then in more recent centuries, people started trying to modify the set of axioms. In some cases, this led to equally consistent and interesting theories. The famous example is “non Euclidean geometry”, as in Einstein’s general relativity. The modern view of axioms is that they are a small set of statements, that in combination with precise rules, define an interesting theory. Perhaps one of these is the theory of our universe.
So it would appear there are lots of different axiomatic systems. BUT: If they are sufficiently sophisticated, Turing complete to be more specific, they can imitate all others, as we will see later.

OK, so what is the Entscheidungsproblem? It asks if all mathematical statements like “31 is a prime number”, can either be proven to be true, or proven to be false. Starting from the axioms, and using only the valid logic rules that we defined beforehand.
In our daily lives, we generally think that statements are generally either true or false. If they are neither, then we get an eerie feeling that something is deeply wrong. So Hilbert felt the answer to the Entscheidungsproblem is probably YES, and that would be a great triumph of mathematics! But a few years after 1928, when Hilbert first posed the question, Gödel proved in 1931 that the answer was NO!

Godel

Kurt Gödel (1906-1978).

He was the first to solve the Entscheidungsproblem. His proof is more difficult to understand than Turing's proof; you have to learn mathematical logic first. Gödel himself had more difficulty with ordinary things in life, like eating (he suffered from fear of being poisoned). When he applied for immigration into the US, he stated that he disagreed with the US constitution, which contained inconsistencies. Luckily, he was accompanied by his friend Einstein, who managed to convince the immigration officer to let him in. (Story slightly simplified for dramatic effect)

Alonzo Church

Alonzo Church (1903-1995)

Church also solved the Entscheidungsproblem slightly before Turing. Moreover, Turing was his student. Like Gödel's proof, Church's work is important for mathematics, but more difficult to understand.

Rado

Tibor Radó (1895 - 1965).

He decided to become mathematician while he was in a Siberian prison camp, from which he escaped. He invented an easy to understand model of a computer using "Rado Cards", that I will use on this web page. He also invented the “Busy beaver game”.

A simple computer
In the animation below, I try to explain the idea of a computer using Radó's cards. It is just like a game: You start with a card, and do what the card tells you to do. This interacts with the symbol on the tape. I hope it is self-explanatory. A card always has 3 instructions in case the present symbol is "0" and likewise 3 instructions for case "1". Instruction 1 is a WRITE, instruction 2 is a MOVE. The 3rd instruction is the number of the next card. There is one special card called "HALT". If you get to that card, the computation is finished, and the symbols on the tape are the thing that you have computed! The example below compute 1101 from a blank tape.

Animation of Rado cards

You could in principle operate this machine powered by a human operator, who does what the cards say. It does not matter in principle if the machine is electronic, mechanical, or human-operated.

Now for a big surprise: How long will it take to get to the HALT card?
In some cases, it is easy to see how long it will take. In some cases also, it is fairly easy to see that the answer is "never".
But for some very simple Rado sets, the answer is UNKNOWN! There are sets of just 6 Rado cards, which have been running for years, but no one knows if they will ever halt! In the meanwhile, they are printing a lot of "1" symbols. The "Nth Busy Beaver number", is the maximum number of ones an N-card Rado set generated when it halts. Rado proved that this number grows faster than any computable function. The Busy Beaver number sequence itself is therefor uncomputable.

NB: To implement a Universal machine using Rado cards, you need quite a few cards. I don't know exactly how many.
These tape-based machines are interesting theoretical things, but it is very unhandy that if you have a portion of tape containing valuable temporary results, you have to step over this cell by cell. Turing used tricks like reserving odd cells for storing valuable information and even cells to guide the movement. Instead of this, modern computers can instantly jump to an address in memory. The downside is that the amount of memory becomes finite, in contrast to the infinite tape.

Universality
OK, we have explained that we can make machines that can do all sorts of things, but how do we know they can be Universal?

Universal information
Can you think of something that cannot be represented by a set of numbers? Text can be represented as numbers (eg ASCII). So can pictures, by specifying the pixels. So can sound, by specifying the air pressure as a function of time. Some might argue that things like "love" cannot be expressed as a sequence of numbers.
As far as I can see, at least all scientific though can in principle be expressed as a sequence of numbers. These numbers can be expressed as a sequence of "1"and "0" symbols, which can be read by a computer.

Universal computation
If all information can be expressed as a sequence of "1" and "0" symbols, then any imaginable information processing operation can be performed by a machines that manipulate these symbols. You might think that for each process, we would need a different machine. But suppose we can describe how the machine works (In modern language, what its program is) in terms of numbers. A Universal machine is a machine that can take the description of what another machine does as input, and then imitate it. To prove that you can make such a machine, Turing had to literally describe how to construct one using basically Rado cards, except he called "cards" "internal states".
This is quite difficult. It is simpler to do if instead of a tape, we can just jump to a place in memory specified by an ADDRESS. The address would be stored in a Register, which is a special memory, reserved for a specific purpose.
In fact, we want a CPU (Central Processing Unit)
This is basically a Rado card whose instruction content can be read from memory. The input and output bits are no longer the bit at the tape position, but can be freely specified by an address register.
We want a register for the READ memory address, the WRITE memory and a register for each item on a Rado card. These new Rado cards are a bit more complex, because they have instructions to manipulate each register, not just the one bit at the tape position. To imitate a Rado card, we have to read the code for the card from memory into the registers. If we know how much data is in one Rado card, say 100 bits, we can put the cards (1,2,3...) in memory at predifined places (100,200,300...)
So we could imitate any set of Rado Cards by placing them in memory, reading them into our CPU registers and executing them. There are details to sort out, and they can be done in many ways. But this web page is for the lazy people, by a lazy author.

Uncomputable numbers and the Entscheidungsproblem
Although a Universal machine can imitate all computation processes, there are certain things that cannot be computed. Turing proved that no program exists that answers the Halting problem: A program that can read another program (P) and then always be able to answer if P will ever halt or not. Sure, for some cases it is possible, even sometime easy to figure out. But a program that can do it for all programs cannot exist. The idea of the proof is actually "simple", but confusing. If such a program existed, call it H, then you could construct a special nasty case that would trick H. This special program would include a copy of H itself, check what H would predict it would do, and then do the opposite. This would lead to a contradiction, so H cannot exist.
This is related to the liar's paradox: "This sentence is false".

How does this solve the Entscheidungsproblem? Well, finding a mathematical proof is a lot like a computation. If you spell the proof out into all its elementary steps, then each step is so well defined it could be done by a machine. So if computers have things they can't compute, then there must also be statements that mathematical methods cannot prove.