Knowable and Unknowable for Universal machines and Humans

Gerard Westendorp, 2019

My website is moving. Best go to the new location at westy31.nl This old page will be gone soon...

Home
Sorry for the bombastic title, but it sounds cool.
I just wrote an article, now trying to get it on the ArXiv, called "Internally Uncomputable functions, with application to the P versus NP problem". If the article is correct, it would solve "P versus NP", an important open problem . Of course, I realize many people have already claimed this before, and till now they were all wrong. Actually, my proof is at this moment probably incomplete, but hoprfully still an interseting approach.

This web page is an informal explanation about the problem, and what I wrote about it. Here is a pdf of the article.

History

In 1900, David Hilbert was probably the most famous mathematician of his time. A new century had just begun. He did not know yet that it would bring 2 world wars, and a huge increase in scientific knowledge. But as for mathematics, he made a good guess about what would be important: Hilbert's 23 problems.

Hilbert, Gödel, Church, Turing and Radó.

Hilbert's 2nd problem (after it was reformulated a bit more carefully) became known as the "Entsheidingsproblem".
It asks:
"Can all of mathematics be formulated in terms of fixed axioms, and fixed derivation rules, so that all mathematical truths can be either proven or disproven using these rules?"
"Can we exclude that something is both provable but its converse is also provable? (ie: can we be sure mathematics is consistent?)"
"Entscheidung" means "distinguish`, in the sense of dividing everything into "TRUE" and "FALSE".
(Note: Hilbert was not the first to ask this question, it was already asked by Leibniz in the 17th century)

This problem is obviously of great interest philosophically. It seems to tell us something important about thought itself. But is it true?
Well, to everyone's shock, in 1935, Kurt Gödel proved that it was false!
Besides TRUE and FALSE, there are certain propositions that are UNDECIDABLE.
Also, mathematics might be consistent, but that cannot be proven within mathematics. And Gödel could prove that it could not be proven!

What can we make of this? One problem was that Gödel's article was quite difficult for those untrained in the language of mathematical logic. Nevertheless, as with most good ideas, the basic idea is actually simple, but subtle. Douglas Hofstadter explains it in his book "Gödel, Escher, Bach".
Gödel's idea was greatly clarified in 1936 by Alan Turing. In the same article, Turing also explained all the basic ideas behind the "Universal machine", now better known as the computer. I am skipping the work of Alonso Church here, but many of Turing's ideas were partially preceded and influenced by Church and others, like Kleene. However, the great advantage of Turing's approach, is that it is much easier to understand than Godel and Church. Why? Because it can be expressed in terms of things that a computer does. That is much easier to visualize, especially for us in the 21rst century.

If you break down mathematical reasoning, at the lowest level it seems come down to applying a fixed set of rules. These rules are so unambiguous, that they could be done by a machine. So Turing thought: What if they are done by a machine? First he described how you could build a Universal machine, one that could simulate any other machine, by adding some extra data: what we now call a "stored program". Then, he showed that there are problems that such a machine cannot decide. One such problem is the Halting problem. It asks for a general procedure for determining if some other programs ever stops (Halts), or goes on forever. For some programs, this is easy to see. But in more complex cases, it gets very difficult. In fact impossible, as Turing showed.
If a Universal machine cannot compute something, then mathematical logic cannot prove that thing, and we humans cannot know if it is true.

How can we know a universal machine exists?

First, we can think about universal data. It is very hard, perhaps impossible, to think of anything in our world that cannot be expressed as a set of numbers. Written text can be converted to numbers, by numbering the characters of the alphabet. Pictures can be turned into numbers by turning them into a bitmap; each pixel is given a value for red, blue and green. Sound can be turned into numbers by specifying the sound pressure for each time step. Physical systems can be turned into numbers by specifying velocities, positions, field strengths, etc.
Note that there is one assumption I brushed over: We have to first discetise things. Well, text is already discrete, but a picture for example could in principle have an infinite number of pixels per area. We assume that very small details become unimportant. Is that true?
Here is what Turing wrote about it in 1936:

It will seem that given the initial state of the machine and the input signals it is always possible to predict all future states, This is reminiscent of Laplace's view that from the complete state of the universe at one moment of time, as described by the positions and velocities of all particles, it should be possible to predict all future states. The prediction which we are considering is, however, rather nearer to practicability than that considered by Laplace. The system of the "universe as a whole" is such that quite small errors in the initial conditions can have an overwhelming effect at a later time. The displacement of a single electron by a billionth of a centimeter at one moment might make the difference between a man being killed by an avalanche a year later, or escaping. It is an essential property of the mechanical systems which we have called "discrete-state machines" that this phenomenon does not occur. Even when we consider the actual physical machines instead of the idealized machines, reasonably accurate knowledge of the state at one moment yields reasonably accurate knowledge any number of steps later.

OK, we are not sure the universe is ultimately discrete. But if we will just concentrate on discrete systems for now. We can go one step further down the reduction ladder: From numbers to bits. Any number can be written as a bunch of "1" and "0" symbols, ore equivalently "TRUE" and "FALSE". Welcome to the digital age!
Now a universal machine has to be able to convert any set of bits to another set of bits.

Consider a digital machine as a black box. In go M bits, out go N bits. We can split the problem of building a universal machine for this, by doing it one output bit at a time. Often not efficient, but conceptually easier to understand. So how can we make any 1-output bit function of M input bits? Well, we could just make a list of all the combinations of the M bits for which the output is TRUE, and otherwise, leave it FALSE. In other words, we write down a Truth table. For example:

A AND (NOT(B)) AND E
  OR B AND (NOT(C))
  OR A AND E
  OR .....

A,B,C,... are the names of the input variables.
Each row is composed of variables, tied together with NOT and AND.
The Consecutive rows can be glued together with OR.

So the only functions on bits that the machine needs are NOT, AND and OR.
To be even more minimalistic, all 3 of these can be made from the function NAND (Not AND):

NOT(x) = NAND(x,x)
AND(x,y) = NAND((NAND(x,y),(NAND(x,y))
OR(x,y) = NAND((NAND(x,x),(NAND(y,y))

In addition to calculating these functions, the universal machine has to be able to read and write to memory. In Turing's original machine, this was done by moving a tape, on which the symbols could be read and/or printed. But let's take advantage of more modern architecture, and just assume that you can do READ(Address), and WRITE(Address). Ultra-minimalistic Turing machines tend to be more tricky to understand.

If a machine can READ(Address), WRITE(Address), do a NAND function, it can in principle do anything. Now we are ready for the final step. Give these basic instructions a code number. Then, write down the sequence of instructions you want the machine to do as a sequence of these numbers: the "Program". If we can build a machine that can read a program instructions, and then execute the instruction, and move to the next program instruction, we have a universal machine! What about machines that have multiple simultaneous processors, or quantum computers? Well, these can be simulated by a universal Turing machine, although sometimes at high computational cost.

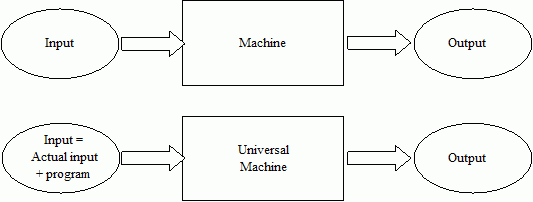A universal Universal machine can simulate any other machine, by adding the "program" of the other machine to the original input.

Things a Universal machine cannot do, and its implications for humans and mathematics.

A Universal machine can simulate logical reasoning and vice versa.
So if has a Universal machine has a problem that it cannot solve, then this means mathematics itself has a problem it can't solve.
A Universal machine can simulate human reasoning and vice versa.
So if has a Universal machine has a problem that it cannot solve, then this means humans have a problem they can't solve.
(I know not everybody agrees with that)

Turing's original argument showing that a machine cannot decide its own halting problem, goes roughly like this:
Suppose there is a program H, that inspects the program of some other program, and after analyzing it, outputs "1" if it halts, and "0" if not. The you can then construct a program H2, that is specifically designed to fool H. It creates a copy of itself, then uses the code of H (which is "public"), to see if H would think if it halts. Then it does the opposite. it is actually a bit tricky, though possible, to give the code of H2 to H, including the intention of H2 to do the opposite H thinks it will do. But even that information cannot help H. What is the big advantage of H2 over H? That H claims to exist, and be capable some very difficult things, while H2 claims only to exist if H exist.

Here is an analogy:
Imagine there is an App on your smart phone that claims it can predict what people will do. You want to know if someone will go left or right, you ask your App, and it will tell you. But now, you ask the App what you will do. It answers "left". At that moment, you seem to have "free will", you could decide to do the opposite. Does that prove free will exists? No, it proves that the App cannot exist. By "Free will" I mean something outside the laws of physics, that we humans might possess, that enables us to make choices that cannot be predicted by by any super smart entity.

I call programs like H and the above App, internal programs. They are themselves part of the system. As such, they are accessible to other internal programs, which can then outsmart them. Given a finite machine (M1), an external program is a program on machine (M2) sufficiently bigger than M1, that is able to simulate M1. For M2, everything on M1 is completely known. M2 knows if M1 can prove something true, false, or if it cannot decide. It also knows with certainty what all programs on M1 will do. And this time, the programs on M1 cannot make use of the services of M2, because it is too big.
In the analogy to humans: The Gods know what we are going to do, but we cannot implement The Gods on an App, because they are too big. The Gods are external to our universe, the app is internal.

The distinction between internal and external programs is the "secret weapon" I used to prove P is not NP.

P versus NP

Have you ever had an "AHA moment"? Suddenly, you see a solution to a problem that had been bothering you for some time. Well, that means your problem was in complexity class NP. The "AHA" solution was verifiable in a short time. But finding it was hard. The P versus NP problem asks if there is a "Eureka generator": An efficient procedure for finding a solution assuming that the solution is quickly verifiable.
If the input of the problem has N bits, then there is a "brute force" method for solving it: Try all combinations. This will take an amount of time that is proportional to 2^N. It takes "exponential time", which means in practice an extremely long time. Try doing a Sudoku by trying all number combinations...
P stands for Polynomial time, which means essentially faster than exponential; it does something smarter than simply trying all possibilities.
NP stands for Non Deterministic Polynomial Time, which means the problem can be solved by "guess and verify".

Venn diagram of complexity classes P and NP.

If a Eureka generator would exist, then P=NP. Given that the problem is verifiable in polynomial time, the Eureka generator will find it in polynomial time. You might say "automate creativity" (If N is not NP, computers can still mimic creativity by "try&verify". But not by one single omnipotent deterministic method)). 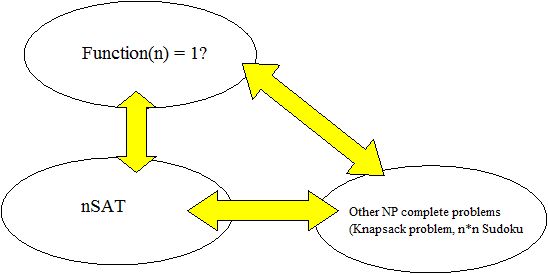By the way, the most sophisticated problems in class NP are all related, they are "NP complete". This was discovered by Cook and Levin 1n 1971. Sufficiently sophisticated problems are a bit like universal machines, they can "simulate" other problems. But that means if you have an efficient solver for any NP complete problem, then you can solve all others too: P=NP. Conversely, if you can prove that one NP complete problem cannot have an efficient solver, then none can, and P is not NP.

All NP complete problems are related, they can be transformed into one another. If one would be in P they all are.

So what did I do?

First, I prove the "bounded time halting theorem". This is like the halting theorem, but now we ask if programs stop in time <T, rather than in unbounded time. This can be decided by a program that is allowed a time sufficiently longer than T: It could simulate the program in question, and see if it halts I call this an external program. But I prove it cannot be decided by an internal program that itself can only use time <T.
This makes undecidability a bit less mysterious. It comes from the fact that you can run out of time trying to find some solution. You can increase the time, but the problems can then also increase in complexity. The solvers are always behind on the problem generators.

Then I look at the NP-complete problem of finding a solution to f(N₁) =1. N₁ is a number with N₀ bits. f is a function, implemented by a program that takes less time than a polynomial function of N₀. So a solution is verifiable in polynomial time, you run f for the N₁, and check if the output is 1.
To find N₁ by brute force, you have to try 2^N₁ possibilities. Finding a solution to f(N₁) =1 is an NP complete problem. It can simulate known NP complete problems.

Suppose there is a smarter way of finding N₁, by a program G.
I call G the Eureka generator for that problem, and assume it also takes polynomial time.
It is sufficient for G to say if a solution f(N₁) =1 exists. If we have such a program, we can then use it again on a modified function, which fixes one of the input bits to "1". If a solution still exists, the bit is correct, if not, it "must be "0". By repeating this, we can find N₁ in polynomial time.

I then use arguments very similar to Turning's original argument, to show that G cannot exist. Because G is an internal program, the program that implements f(N₁) could make use of it, and then fool it. I have to be a bit careful about the computation time. f has to run in polynom,ial time, so it can call an internal version of G, that itself also runs in polynomial time. It can not however, call an external version of G, because then f would no longer run in polynomial time.
So a polynomial time version of G cannot exist, but an exponential time version can.
(Actually, I proved that the time G is forced to sometimes take, is larger than the verification time, and the verification time may be artificially increased. Its a bit unclear if this really means P is not NP. Still working on that...)

What about Baker, Gill and Solovay?

In 1975, Baker, Gill and Solovay wrote a paper in which they argued that "diagonal arguments", like the ones I use, have a problem. Basically, if your proof would continue to work even if your machine had an "Oracle", a kind of magical instruction that gives you the solution to some problem in one step, then you are in trouble. Because if the oracle was a Eureka generator, then your proof says opposite of the very definition of the oracle, namely that the Eureka generator does not exist. They call this "relativisation" of the proof.

Luckily, I have my secret weapon, the internal versus external distinction.

If the oracle is internal, an actual instruction on M₁, then the problems are also allowed to use it. The advantage of G then disappears. It was already known for the Halting problem, that even oracles cannot help if the programs themselves have also have access to the oracle. This is the case for the problem I chose, which concerns programs, rather than "static" problems, that cannot simply call an oracle.

If the oracle is external, then yes, the Eureka Generator would work. This asymmetric warfare situation seems to exist when the solver is a computer with access to the oracle, but the problem is a static puzzle for example a Sudoku puzzle. In his 1971 article Cook showed that the condition that a computer solves something, can in fact be cast into conditions inside NP complete problems. If the oracle was based on brute force search, then casting that into a Sudoku, by adding extra columns and rows, would create a very large Sudoku, exponential in the size of the original one.
The fact that an P=NP with an external oracle does not contradict my proof, because by giving a tool to the solver and not to the problem, the reasoning in the proof changes, so the proof does not "relativize".

The 5th man

The picture galley at the start of this web page has one person I have not mentioned yet: Radó. He invented the Busy Beaver Game. First, he constructed a Turing machine that works with a tape, and very simple "Cards". The cards tell you what to do, dependent on the symbol on the tape: A combination of
1.move the tape
2.print a symbol on the tape
3.go to another card (the cards are numbered)
Then using a small set of cards, he asks how many times the program will write "1" on the tape, before it halts.
The winner of this game, for a fixed number of cards and allowed tape symbols, is the Busy Beaver.
It turns out these busy beavers are wild, unpredictable programs. Even a very simple set of cards, can generate a huge number of "1"s. And for some very simple ones, no one even knows if they halt! For example, according to Wikipedia, the 4 symbol. 3 card Busy Beaver does not have a definite winner yet, but so far the best Beaver has printed >3.7×10⁶⁵¹⁸ 1's!
The reason I include this is that there seems to be stuff beyond NP complete problems.
But I don't understand that yet.