Error
correcting code and
symmetry.
 Starring Golay
codes, the
sporadic symmetry group Mathieu 24 (M24), and
the
Leech lattice, which is the
"one
lattice of power" that rules all other lattices from its 24 dimensional
throne.
Starring Golay
codes, the
sporadic symmetry group Mathieu 24 (M24), and
the
Leech lattice, which is the
"one
lattice of power" that rules all other lattices from its 24 dimensional
throne.
With a guest role for Klein's Quartic.
(home)
I started this page after brooding on the intriguing fact
that
apparently, a devilishly smart way of doing error tolerant digital
signal transmission, called the Golay code, is related to the magical
symmetry group M24.

My curiosity for M24 was sparked by
remarks like this
one in the
Atlas
of Finite groups
(A famous big red book that I bought, in the hope to understand it one
day ):
"The group M24 is one of the
most remarkable of all finite groups. Many properties of the larger
sporadic groups reduce on examination to properties of M24. This
centenarian group can still startle us with its youthful
acrobatics." The
3D
print on top of
the book is a great dodecahedron, which we will encounter in a minute.
There are many maddeningly
fascinating references to M24, and
the Leech
lattice, but to understand this, you have to pass through some daunting
mountains of difficult mathematics. Until I found the secret passage
that I describe on this page. Read on...
The error detecting trick I already knew was the "parity
bit". This occurs in the old RS232 code, where you have to type config
parameters things like 7,1,e. That means 7 data bits, 1 parity bit,
even parity. Sometimes, if the connection does not work, you have to
change this, although usually this is taken care of by higher level
software.
The idea of parity
check
is simple, you count the number of 1's, and then add a parity bit, to
ensure the total amount of 1's is even (or odd, if you want odd
parity). This allows you to detect errors. If one bit gets
flipped, then the parity will no longer be correct. In practice,
you would do some kind of RESEND request to the other side. But if the
other side is a spacecraft 4 light hours away on a Pluto mission it
will be helpful if you can correct the data yourself.
The trick to correct errors as well as detect them, is related
to
geometry. Below is a picture of a polyhedron, in this case a cube.
Imagine the data bits are placed on the vertices, and on each of the
faces is 1
parity check bit. They are the parity bit on the 4 bits on the
vertices contained in the face. So this code would have 8 data
bits and 6 parity bits.

Data bits on the vertices, and parity check bits on the faces, which
detect and locate an error for correction.
You can now see the magic trick: If a data bit on a vertex flips, then
all 3 faces
that contain this vertex will fail the parity check. From these 3
faces, you can find the failed bit, it is on the intersection of the 3
faces. Also, you can know if a parity bit itself fails, because there
would
be only one parity error, while they should always come in sets of 3 if
they are the result of 1 failed data bit.
With the cubical code, we can almost detect and correct 2 errors, but
it turns out you can figure out an unlucky combination that it cannot
distinguish from another.
Note1:
We alway assume
there is some maximum number of errors per block. Given unlimited
errors, you can screw up anything.
A natural question to ask is, how much better can we do than the
cubical code? I don't know if Golay was on the same line of thought,
but in 1949 he set out to find the ultimate code. Golay's
original
article is very
short, only half a page:
http://www.maths.manchester.ac.uk/~ybazlov/code/golay_paper.pdf
Because of its conciseness I was hoping to understand it quickly. He
writes that he found his code by looking for a row of Pascal's triangle
whose first few entries add up to an exact power of 2. It was at first
not clear to me how Pascal's triangle comes in. Golay perhaps
overdid the conciseness somewhat by not explaining this.
But I get it now:
Suppose you have N parity check bits in a block of M bits. You can
maximally encode 2N
distinct facts with these
parity
bits. You want to optimally encode the error positions:
The number of possible error positions of 0 errors is 1
The number of possible error positions of 1 errors is M
The number of possible error positions of 2 errors is M(M-1)/2
The number of possible error positions of 3 errors is M(M-1)(M-2)/2/3
These combinatorial numbers are just the (M+1)th row of Pascal's
triangle. (Aha, Golay said M, so he is human too).
Row 24 gives: 1, 23, 23*22/2=253, 23*22*21/2/3=1771, which adds up to
2048, which is 211
.
So if
you can find a scheme with 12 data bits and 11 parity bits that
describes up to 3 errors, then you know for sure this is optimal,
because 11 bits cannot possible encode more data than that which is
needed to describe the errors.
Golay then goes on to supply a scheme for identifying up to 3 errors,
using the so-called "generator matrix". This is just a n M*(M-N)
matrix, with which you multiply modulo 2 with the data bits, to get the
M (data+checksum) bits. Matrix multiplying modulo 2 is actually
equivalent to just doing a parity count of the rows of the left matrix,
masked by the columns of the second matrix. Once you try it, you will
see it is easy.
To help get used to generator matrices, here are the generator
matrix for the "cube code" in our animation, and for a simple parity
check. They are
written in such a way that you need to put your data bits as a row
vector, multiplied on the right side by the generator matrix, which
then gives the new (data+parity) as a row vector.
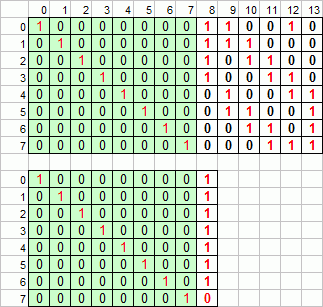
Generator
matrix for the "cube code", and
for a simple parity check.
Golay figured out the optimal code for 23 bits, called the "Perfect
Binary Golay code", but often, one extra bit is added, to get the 24
bit "Extended Binary Golay Code". This one is in fact a little more
wasteful, but its relation to symmetry is more clear. We will use
the Extended Binary Golay Code, whose generator matrix is
given on
Wikipedia:

(Wikipedia
image), Generator matrix for the extended binary Golay
code.
Now this matrix corresponds to a polyhedral code on the [suspense
music building up...] great
dodecahedron!
The great dodecahedron is perhaps not the most famous polyhedron, but
is actually special in a couple of ways. It has 12 vertices and 12
faces (12 pentagons that intersect each other). So its number of faces
is equal to its number of vertices. It also has 5 vertices per face,
and 5 faces per vertex, so it has this additional face/vertex symmetry.
These 2 feats are pulled off by only 1other uniform polyhedron: the
small stellated dodecahedron. But that one is more or less the same
polyhedron, with the vertices reconnected differently. Indeed, as
Refurio Anachro pointed out, they are each other's dual.

Great dodecahedron
If we worked the same way as with the cube, doing a parity sum
for
each face, we get all the ones and zeros exactly opposite
to the Golay code. So what
we have to do is for each face, parity sum all vertices except
those contained by it. This
means each of the 12 faces does a parity sum over 7 vertices. Count the
ones in each row of the Golay generator matrix, they are all 8. Below
is an animation of a failed bit (green blinking disk on the pentagonal
face), and the 7 awakened parity checks (red blinking). I put the data
bits on the faces this time, and the parity bits on the vertices, for
greater clarity. One of the symmetries if the Golay code is that you
can interchange the faces and the vertices and parity/data.
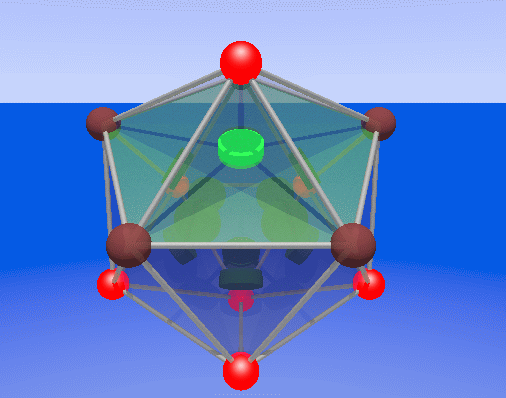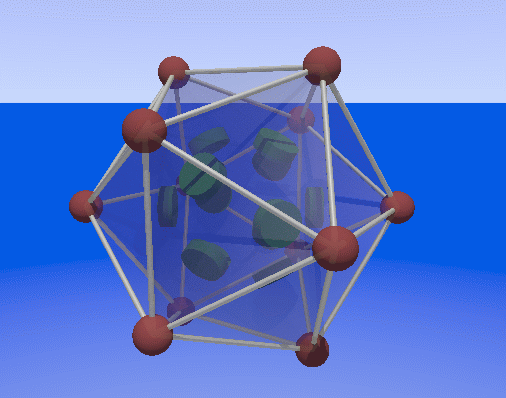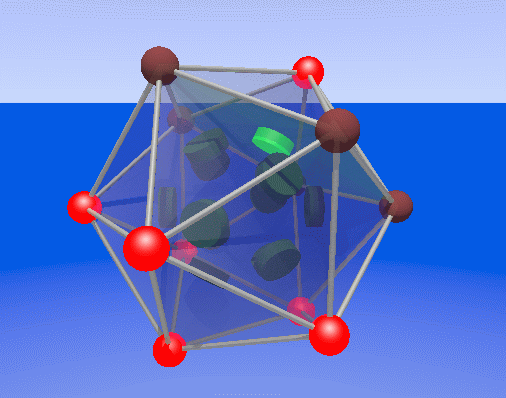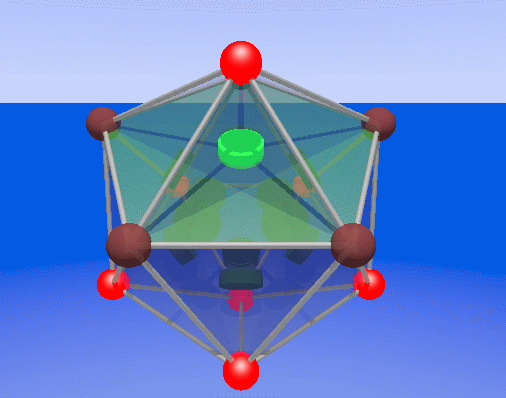
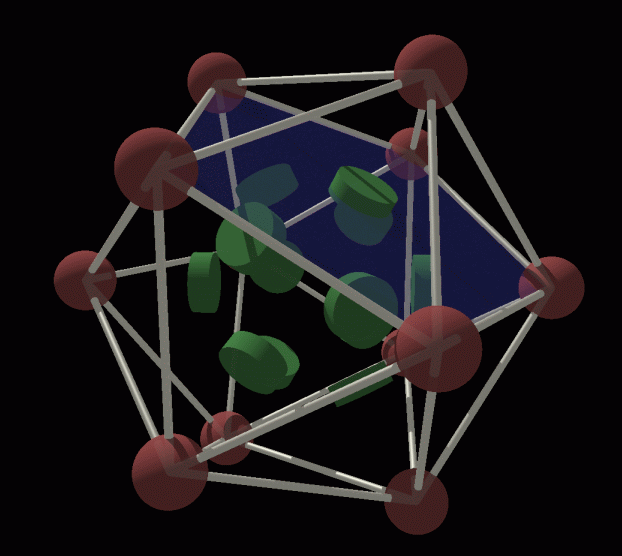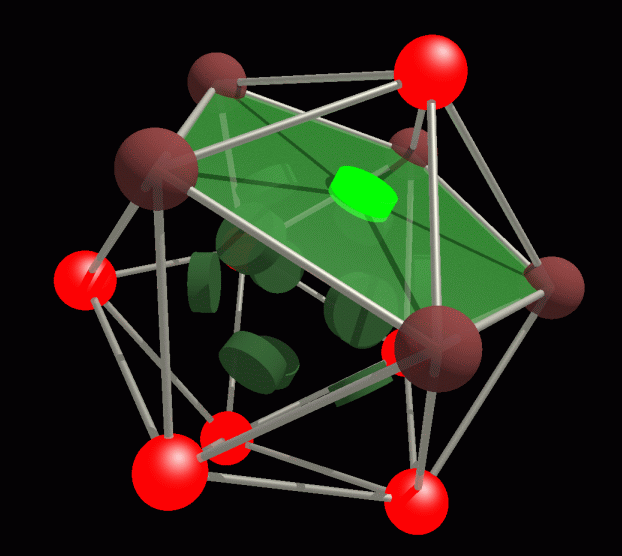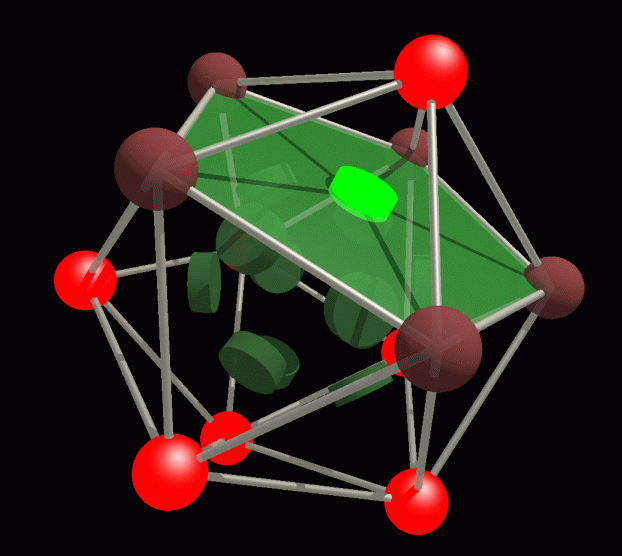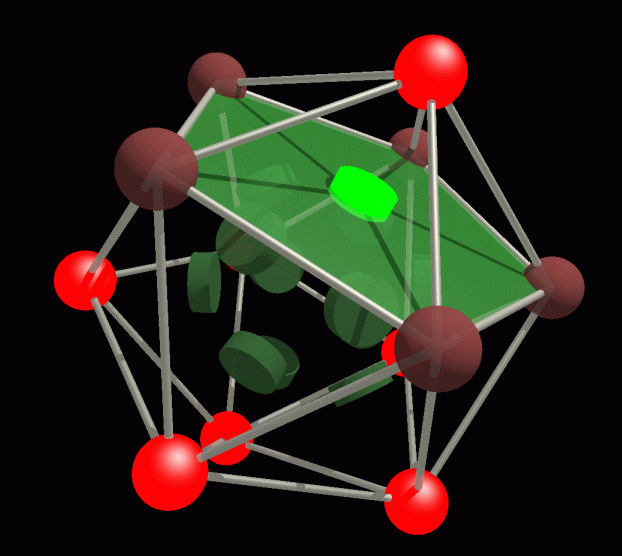
Animations of the data bits on the great dodecahedral faces, with
an error (green flash), and the parity check alarms (red
flash) on
the vertices.
So we've done it! We have an easy to visualize interpretation of the
Golay code.
The
Leech
lattice
Let us now define the Leech lattice in a way we can understand. In 24
dimensional space, you can consider all points with integer
coordinates. These form a 24 dimensional hypercubical lattice,
which does not seem so special.
But what if you keep only points whose coordinates are related to the
Golay code? That is basically the idea that Leech had back in 1964.
This new lattice would after rescaling by the distance between 2
neighbours, be much denser. Leech knew his lattice would be highly
symmetrical, but he did not know enough group theory to figure out the
symmetry group. He tried to interest group theorists and eventually
Conway ended up solving it, resulting in the discovery of 3 sporadic groups
Co1, Co2, and Co3.
One feature of Golay codes is that the minimum squared distance between
2 valid words is 8. Leech wanted to retain this property in his
lattice. So he could not just take all integers modulo 2, and
check if that is a legal Golay word. Because then you could
for
example replace any '0'by '2', to get another lattice point, which
would be at squared distance 4.
At this point, we will multiply all numbers by 2, for later
convenience. So Golay words are now doubled eg(0,2,0,0,2...)
and
the minimum squared distance between two words is 32.
Then, changing by 8 is OK (squared distance 64). In fact the Leech
lattice is periodic by translations of 8 integers in each direction. In
the matrix below, the first row vector is an example of such a
translation.
Another translation that would be allowed is 2 translations by 4, in 2
different directions. Examples of these can also be seen in the matrix
below. This would lead to words that are strings of '0','2','4'
and '6'. These even points are just half the points of the Leech
lattice. Interestingly, Leech first left it at that. But about
a
year later he doubled the density by adding also odd points (See now
why we multiplied the points by 2). If you take an even Golay word and
make all even numbers odd , then the new word will be at a
squared
distance of 24. So shift one coordinate by 3 instead of 1: Squared
distance 23+9=32! This is implemented by the bottom row of the matrix
below.You can of course choose any coordinate to shift by 3 instead of
the first one, but these vectors can be formed by linear combinations
of the others.
Another way to see it is to represent the coordinates modulo 8 as 3
bits, (000,001,010,011,100,101,110,111). So for each point, you have 24
numbers of 3 bits. Then, the middle bits have to form Golay words. The
least significant bit must either be all 24 ones (odd points) or 24 all
zeros (even points). The highest of the 3 bits can be anything, except
the even points need to have an even number of ones, while the odd
points require an odd number of ones. ( I got that from an article
by Austin Roberts)
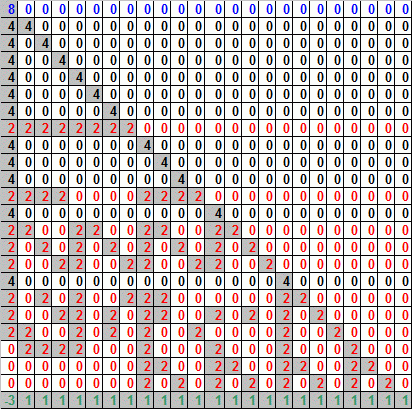
24 row vectors that generate the Leech lattice. The vectors are
arranged so the upper right triangle of the matrix is zero. This
ensures that each new row is linearly independent of the previous ones,
since it is the first to use a new column. The first (blue) row is a
translation by 8. All translations by multiples of 8 are allowed,
others can be made by linear combinations. The red rows are 11 legal
Golay words multiplied by 2, which together with row 1 (the
zero
word mod 8) generate all Golay words multiplied by 2. The
black
vectors are translations by 4 in 2 different directions. Finally, the
bottom green vector jumps from the even points to the odd
points,
while changing one coordinate by by an extra 4.
I could now go on to find and write amazing facts
about the Leech
lattice, but I run out of time. Conway and Sloane wrote a book on
sphere packings, and in the
introduction they mention that they considered making a special
abbreviation for "It is a truly remarkable fact that", because they
were so often amazed by the properties of packings.
Note2:
This might be a
good place to introduce the buzzword "Hamming weight".
This is
just the minimum number of different bits between 2 valid words. So for
plain code, the Hamming weight is1. But with a parity check, it becomes
2, because if you change one bit, you must also change the parity. For
the cube code shown above, it is 4. For the (extended) Golay code it
is 8. If you look N-dimensional space whose coordinates are the N
bits of a code block, then you can draw an N-dimensional sphere around
the valid word, with a radius related to the Hamming weight. All
words inside that sphere, except the center, will be illegal words, ie
one with a bad parity check. The Golay code has the
property that all possible bit combinations, plotted out in the N
dimensional space, fall inside a spheres centered around a legal
words. This can be interpreted as "correcting" the surrounding words to
the word
in
the sphere center. You can see that this will work especially well with
dense packings, and the densest known packings in any dimension
<=24
is the
Leech lattice!
M24
The group M24 was discovered by Mathieu somewhere around 1870. All
finite simple (ie not built from combining other groups) groups have
now been classified, a work of decades. They come in
families, but there are 26
"sporadic groups",
which do not fit in. The
Mathieu groups are the oldest of these. More and more, people are
discovering strange things about sporadic groups, such as monstrous
moonshine.
M24 is the "automorphism group" of the Golay code: the set of all ways
to manipulate the order of the bits without destroying the structure of
the code. Since we now can visualize the Golay code, maybe we can start
to understand M24. I think I will put this page on the web first, and
then start thinking about M24. A bit of low hanging fruit:
-You can switch the data bits and the parity bits: If you ask which
data bits correspond to a pattern of parity bits, this is just the
parity pattern you get by entering the parity pattern as data!
- The word with 24 zero's, or with 24 ones, are both legal words. All
other words have 8, 12 or 16 ones.
Klein's
Quartic
Klein's quartic is a cherished object in discussions
around the Internet, I spent quite a bit of time making models of it
and
trying to understand it. It is a highly symmetrical figure with 24
heptagons. To see the connection with Golay codes, note that in Golay
codes, each data bit has 7 parity bits "connected" to it, and vice
versa, just like the heptagonal structure in Klein quartic. The total
number of bits is 24, just like the number of vertices of the Klein
Quartic. However, the connectivity is different to the usual Klein
Quartic, which is tiled by {7,3}, each vertex has 3 heptagons. The
Golay code has four heptagons meeting at each point. This allows a
partitioning of the heptagons into 2 groups of 12, colored blue and
green: If the data bits are imagined on the green heptagons, than the
blue
heptagons contain the parity sums of the surrounding data
bits.

Klein Quartic tiled with {7,4}. If the data bits are imagined on the
green heptagons, then the blue heptagons contain the parity sums of
the surrounding data bits.
Note the outer heptagons are cut up into 7 wedges each, each wedge
attached to a neighbour on the 'fundamental polygon'

Stellating the Klein Quartic You get a figure with 24 heptagrams, and
at each vertex now 7 heptagrams meet, and the genus goes from 3 to 19!
(Not all heptagrams are drawn)
links
Part of this work made it to
the American Mathematical Society
weblog 'Visual Insight':
http://blogs.ams.org/visualinsight/2015/12/01/golay-code/
Joe fields has a nice web
page in which the Golay code is
explained with dodecahedra. Masks are used rather than relating
vertices to faces:
http://giam.southernct.edu/DecodingGolay/introduction.html
David Richter has a nice page on M24 and Klein's Quartic:
http://homepages.wmich.edu/~drichter/mathieu.htm
There is a
page
(In Dutch) about Golay.
Apparently, he was for a time a professor
in Eindhoven, where he was a legend. Also, I read he worked on electric
network analogies, so I should
definitely like him!
A short bibliography on John leech. It is interesting to read how he
discovered the leech lattice, but that finding its
properties,
like they are known today, was not at all easy, even for Leech himself.
the definitive form of the lattice took several years (1964-1967), and
to find its symmetry group he tried to lure others until finally Conway
took the bait:
http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Leech.html
http://www.math.ups.edu/~bryans/Current/Journal_Spring_2006/ARoberts_LeechLattice.pdf
http://www.ams.org/notices/201309/rnoti-p1168.pdf










