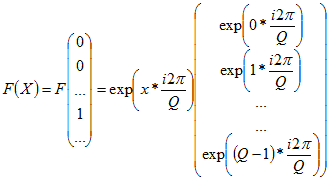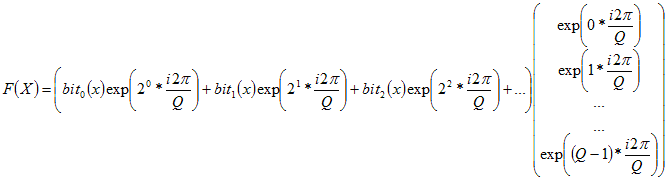RSA
cryptography and how
Quantum Computers could crack it.
 Gerard Westendorp
Gerard Westendorp
june 2018
Other
stuff by me.
RSA encryption is probably the most famous and widely used
encryption
method in the world. It is named after Rivest, Shamir and
Adleman. In 1977, these authors wrote to Scientific American columnist
Martin Gardner, who put it in his legendary "Mathematical Games"
column. It was then called "Trapdoor ciphers". Next, the NSA tried to
stop further publication, which was of course hopeless, due to the
popularity of Martin Gardner's column.
One reason Quantum computers are fascinating is, as Scott Aaronson puts
it: They offer the clearest language to study the strange nature of
quantum mechanics.
The interest in quantum computers got a big boost when Peter Shor
discovered that Quantum computers could crack RSA, using 'Shor's
algorithm!
It took me a while to understand this. There are already quite a few
other websites explaining it, but anyway, here is my version.
So how does RSA work?
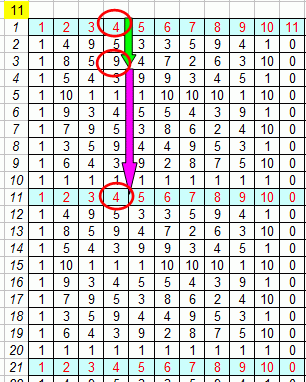
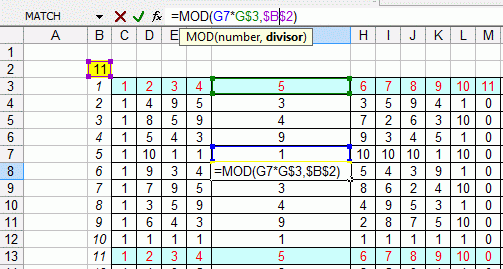
To start with an example, below is a table of numbers. The
numbers are powers of the first row, modulo 11. It is not too hard to
make in a spreadsheet, on the right side is the only formula I entered
to generate it.
An easy way to understand modulo arithmetic is to start with modulo
10. Modulo 10 means looking only at the last digit of the
number in our usual base 10 notation, and simply throwing away the
rest. So for example 9 * 9 = 1 in modulo 10.
Modulo 11 is the same idea, you throw away multiples of 11 until you
are left with a number less than 11.
To hammer this in, it will help to check some table entries by hand,
you will get the idea.
You could use this table for encryption: 1. You encode your message as
a series of numbers from 0-11. (Normally
you would use a number much larger than 11, so you could use blocks of
ASCII)
2. Raise each number to a power mod 11, in our example to the power of
3.
You have finished encrypting!
It might even be a reasonable way to encrypt, as long as you don't tell
anyone except yourself and the receiver how it works.
To decrypt, we can use the fact the the table is periodic. In
our modulo 11 example, we notice that after raising to the 10th power,
we are back to the original number.
So the inverse of raising to the power of 3 modulo 11, is to continue
power raising another 7 rows.
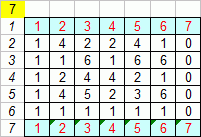
In fact, this works modulo any prime (p):
The period is (p-1).
For example, here is modulo 7.
That was discovered by Fermat, famous for his 'Last Theorem'.
Side note 1:
These tables make it hard for integers to defy Fermats Last Theorem.
For example, the 3rd powers modulo 7 are always 0, 1 or 6. That means
that at least one of the integers in a3+b3=c3
must divide 7!. I once tried to prove Fermats Last theorem by
combinations of these constructions.
Side
note 2: This can
be used to check that a number is prime reasonably fast!
Compared to the full RSA encryption, this method has the drawback that
once you tell the encrypter how to do it, he will be able to decrypt as
well as you can.
But to get RSA encryption, we go one step further.
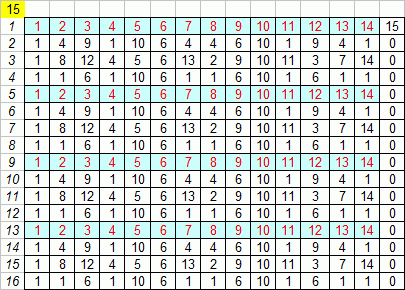
Below is a table modulo 15. 15 is a product of 2 primes, 5*3. The
period is now 4, as we see in the table below.
Why is the period 4? Well, 4 is the lowest common multiple of
(5-1) and
(3-1). It turns out that this is the general rule for the period of any
such table. (I 'm skipping the proof, but you will find that on other
sites if you are interested)
And now we can do something cool.
We take to large primes, p
and q,
we multiply them together, N
= p*q.
Then, we tell anyone in the world our Public
Key. That is, the
number N,
and a power that we choose to exponentiate to. So anyone with that
information can encrypt stuff, but decrypting it is very hard for
anyone except us. Because only we know that N
= p*q,
the "Private Key"
Huh?
Well, because we know N
= p*q
we can figure out the period of exponentiation modulo N,
so we can invert the encryption. The period will be a large
number. But for a known power, you can go up very fast, for example by
repeated squaring.
What if you don't know that N
= p*q?
Well, you could try finding the period by exponentiating some number,
say 3, modulo N many
times until finally, you get back to 3. But, N is
very large, and you cannot use the repeated squaring trick that the
owner of the key can, because you might just be skipping your needle in
the haystack.
This is RSA encryption!
And you can also do something else, called a digital signature. You
could ask someone with the private key to inverse-encrypt a message,
and then you could verify with your public key, by re-encrypting it,
that the other side actually has the private key, without him revealing
the private key.
Enter quantum computers
My favorite way to understand physics is to make a computer
simulation of it. But quantum mechanics is hard to model on a
computer. One problem is that the state of a quantum system
is often understood as a superposition of many classical
states, so the number of variables you need to keep track of gets huge.
From this came the idea of turning it around: what if a quantum system
could operate as a computer? Would that perhaps yield an
incredibly powerful computer?
Well, superficially it may seem that although yes, quantum computers
seem to work like many classical computers in parallel, but when you
actually ask for the output, the superposition 'collapses', you get one
particular realization, that looks just like an ordinary classical
computer. So do these superpositions really exist? Till now, it looks
like some experiments just cannot be explained unless the answer is
yes. This is the central strangeness of Quantum mechanics,
Schrodinger's cat, entanglement, EPR, etc. Physics has been debating
this for a century. And now quantum computers actually propose to use
this strangeness.
The thing is, before a quantum superposition collapses by a
measurement, the terms of the superpositions can interfere,
and cause some outcomes to be more likely than others. That is what
Shor's algorithm utilizes.
An important point is perhaps "Forget about qubits!"
Sometimes
quantum
computers are introduced by replacing the idea of "bits"
by "qubits", which can be in a superposition of 1 and 0. But,
when you perform operations on qubits, the correct mathematical
description of the outcome should be interpreted as "a
quantum superposition of classical computers" rather than "a computer
of quantum superpositions of bits (Qubits)". For example, the no-cloning
theorem says that you cannot
copy a qubit. However, a quantum computer can do copy: When it copies a
qubit, you do not get a copy of the qubit, but a
superposition of 2 computers, one of which copied a "1" , the
other a "0".
The problem is, a superposition of M-bit
computers has 2M
terms in the superposition! Hard to model.
But apart from that, the interpretation of a quantum computer as a
superposition of classical computers does have a conceptual advantage:
classical computers are a lot easier to understand, and each term in
the superpositions is simply doing the same thing as a classical
computer. The strangeness is actually postponed to the "measurement".
The word "measurement" here is used in a broad sense: It means
that the universe has entered into a state in which the quantum system
under consideration can no longer be seen as isolated, but has shared
its information with the rest of the universe. Using other terminology,
the system and the universe have become "entangled". Of
course, they always had been entangled, but after the measurement, the
concept of ideal separation can no longer be applied as a good
approximation.
So how does Shor's algorithm
work?
We do not need to actually factor N,
but it turns out Shor's algorithm allows us to go straight to
finding the period. (Although after finding the period, we will have
done most of the work for factoring)
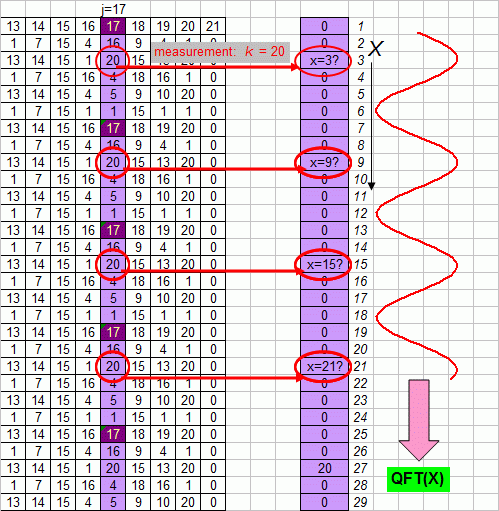
We want to find the period of a column (j)
in our table. It does not really matter which j,
but not one that is divisible by p
or q.
We let the quantum computer calculate k
= jx
mod N.
ie a cell in our table, column k and
row x.
The bits of x
have been put in a superposition using a Hadamard
gate for each bit. In other
words, we are
computing column of our table, with each cell being computed by a term
in the superposition of classical computers. Oh yes, and we take at
least twice the
number of bits in x,
so that we get lots of periods in our column. Define Q as
the oversized version of N.
Then, we measure
k,
without
looking at x.
Because of this measurement, all values of x
that did not produce k
are suddenly zapped out of the universe. (Thats not me trying to be
funny, it is how nature really seems to work!). But x
is still in a remnant superposition, because the possible values of x
are periodic with the very period we are trying to find. If only we
could do some kind of Fourier transform of these superpositioned values
of x...then
we would know the period. (The picture at the bottom tries to
illustrate the idea)
But as I explained above, each term of the superposition in the quantum
computer is just a classical computer, which would just have one x.
So it would not seem to make sense to compute the Fourier transform.
But we do it anyway.
Ahhhhhh... but Fourier transforms are linear! So F(X1
+ X2
+X3
+...) = F(X1)
+ F(X2)
+ F(X3)
+ ....
Here, Xi
is a column with Q elements,
that is zero
everywhere, but has a "1" for row xi.
So because of the linearity of the Fourier transorm, we can do just one
case per classical computer and later, when we measure, we sum over all
states, and get the
right answer.
Unfortunately a Fourier transform would need a Q*Q
matrix. and Q
is a huge
number, so we need to think further.
The Fourier transform that each term in the superposition has to do is
of a very simple kind, it is a column of zero's, with just one non-zero
value at position x.
The Fourier transform of that is:
The column vector is huge, but its structure is extremely simple!
We can go even further. Again exploiting linearity, we break down x
into its binary expansion (we
look at its bits):
Now the answer looks like a couple of phase-shifted bits, all
multiplied by the same huge, but very simple, vector. Can't we just
ignore that vector?
Yes we can! The big vector does not contain any useful information.We
just phase shift each of the bits by the specified amount physically,
by a piece of
hardware called a controlled phase shift gate.
Then, we measure the bits. They will give the correct period with a
high probability, because all the other versions of the period
interfere destructively on average.
This trick is called the Quantum
Fourier transform. It is the key
ingredient of Shor's algorithm.
Ready!
Below
is an artist's impression of Shor's algorithm, which I use on Google
plus to illustrate a post about this web site.
Why it won't work in practice
The quantum Fourier transform uses phase shifts exp(i2π/Q),
where Q
is a number with 2 times as
many
bits as N.
If Q
is a very large
number, then this phase shift is extremely small, say exp(i 0.000000000000000000....3567484...)
LIGO, the machine that detected gravitational waves, manages to detect
a phase change of something like 10-20.
But LIGO only
had to distinguish this phase change from zero. A quantum Fourier
transform needs that phase shift also to be very accurate, otherwise
the interference will get messed up. And, it is currently standard to
have 4096 bits of Q,
how will
you ever do phase shifts that small and that accurate?
Even so, we should continue working on quantum computers, they are so
interesting that something will come out, although perhaps not cracking
RSA in a practical sense.
I'm of course not the only one explaining this. I won't give all the
links, since they are easy to google. But this one
by
Scott Aaronson is pretty nice.