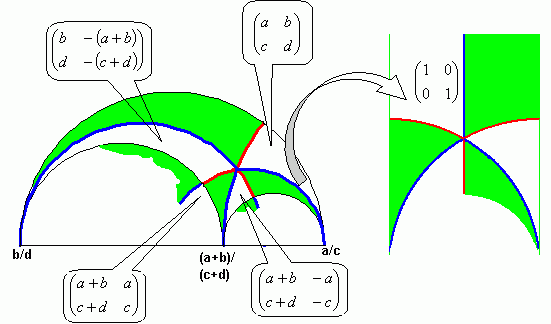
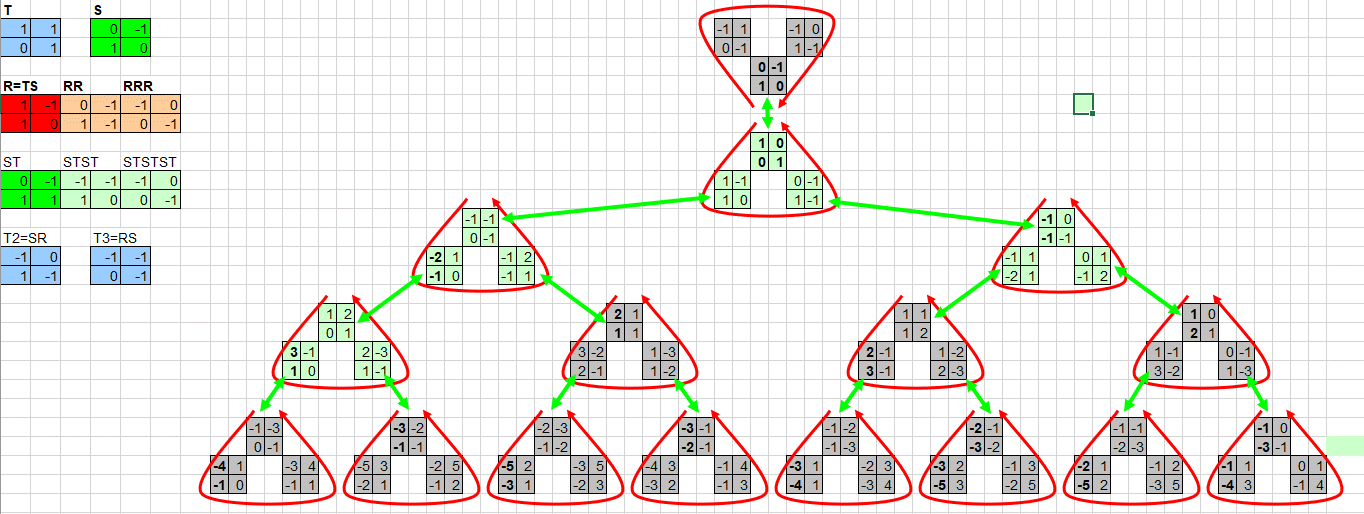
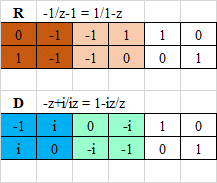
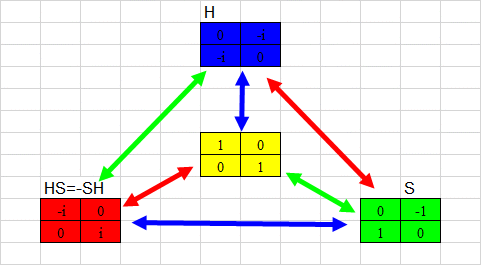
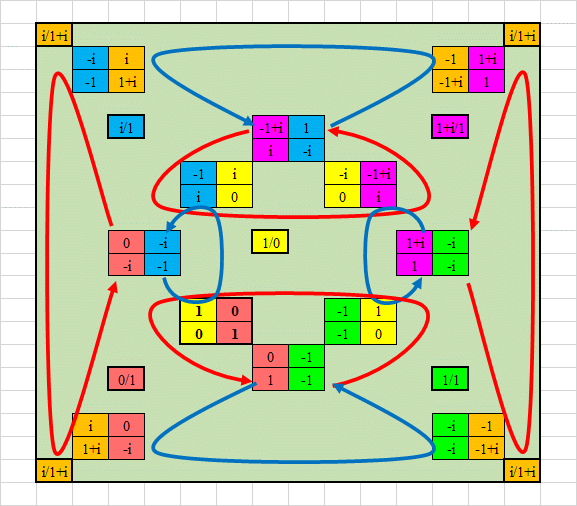
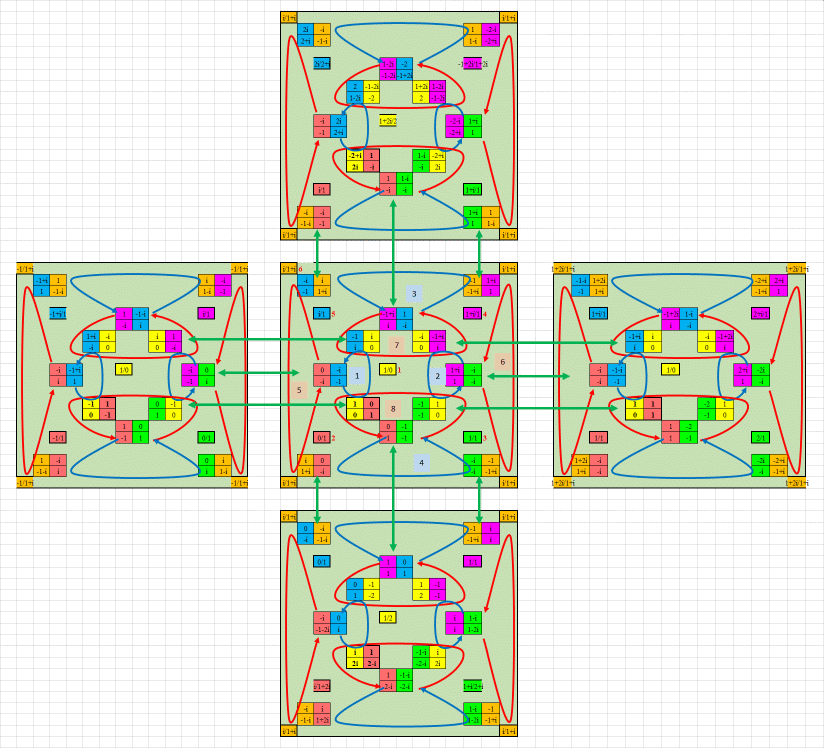
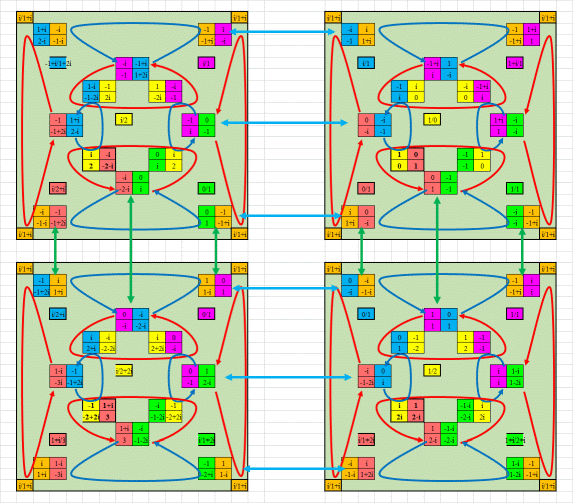
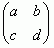The complex Farey fraction tessellation

My website is moving. Best go to the new location at westy31.nl/ComplexFarey/ComplexFarey.html This old page will be gone soon...

Introduction

This page is about a generalization of a famous mathematical object called the Modular group.
I will call it "the Complex Farey tessellation". The Complex Farey tessellation is a known concept, but there are very few pictures of it.
Until now!

I talk more about the modular group on another web page, but I'll mention a few facts, so that you can understand what the generalization is.
The Modular group has connections to many other famous subjects. The Riemann hypothesis, Fermats last theorem, Monstrous Moonshine, to name a few. So perhaps this generalization could give new clues about cool stuff?

Here is a first picture of which the Complex Farey tessellation.

Brief review of the Modular group

There is a picture associated with the Modular group called the Dedekind tessellation. It consists of triangles with circular sides. The angles of each triangle are π/2, π/3 and π/∞.
.

The tessellation is on the upper half of the complex plane; the real axis is the bottom boundary.
Each green or white triangle corresponds exactly to 1 matrix with integer entries, and determinant 1:

These matrices form the modular group.

The geometric operation that corresponds to matrix multiplication is pairs of inversions ("reflections") in the circular sides of a triangle. A single reflection maps a green triangle to a white triangle,and a second reflection then goes from green to green or white to white, hence they come in pairs.

So geometry corresponds to integer matrix algebra:

The triangles all touch the real axis with their π/∞ vertices. These points are exactly the rational numbers! The numerator and denominator of the rational number correspond to columns of the Modular group matrix of the corresponding triangle. These fractions are called Farey fractions. The Modular group "knows" which integers are relatively prime; each rational number occurs exactly once as a Farey fraction!.

Cayley graph

The complex Farey tessellation is what you get when you replace the integers by Gaussian integers. A Gaussian integer is a "complex integer" (a+ib).

To construct the generalization, we start with a Cayley graph of the Modular group.

To make a Cayley graph, you choose a set of generators, and assign a color to each generator. Start with the identity element, and draw an arrow for each generator to the corresponding element. We do not allow duplicate elements. In this way, we will get all elements of the group, together with a nice structure.
Depending on how we choose the generators, the Cayley graph can look different, but ultimately it represents the same structure.

So the Cayley graph of the modular group is a kind of infinite tree, with a 3-cycle at each node of the tree. With a bit of imagination, we can see that the 3-cycles correspond to the triangles in the Dedekind tessellation, and the tree is the infinite hierarchy of the tessellation.

The Cayley graph for the complex Farey tessellation

Now for the generalization to Gaussian integers (a+ib).

There are now 2 3-cycles:

The 2 cycles are interesting, they correspond to Pauli matrices, (multiplied by i) and unit quaternions. We can choose 2 of them, and make this Cayley graph of a subgroup: of order 4:

If we combine the 2 3-cycles, we get a Cayley graph subgroup of order 12:

This subgroup can be interpreted as an octahedron. The 8 3-cycles correspond to the 8 faces of the octahedron. The 12 matrices correspond to the 12 edges of the octahedron. The 6 vertices correspond to 6 Farey fractions, which are the common columns of 4 matrices which are in a 4-cycle RDRD.

Next, if we combine the octahedron with the 2 cycle S, we get an infinite tree of octahedra, joined by "DS-joints":

The combination of R and S gives RSRS=1. So only half the sides of the octahedron take part in this tree. But there is a second tree, with "RH-joints". I will not draw it here, it is similar to the "DS-tree".

The 2 trees partially overlap, through 4 cycles SHSH=1.

The overall Cayley graph is not easy to depict in 2D, it is a 3D honeycomb. We'll go straight to the honeycomb itself, which has the same structure as the Cayley graph.
Start with the Fundamental octahedron:

Next, we apply "DS joints" to the odd faces and "RH joints" to the even faces. These correspond geometrically to inversions in the octahedron faces, combined with an inversion through the octahedron itself . (We need always 2 inversions, to get an operation with determinant 1 instead of -1).

If we add the next generation of octahedra, we can already see there will be overlapping ones.

So we are in business, we can repeat the procedure, and get our tessellation:

Animated Gif of the complex Farey tesselation

This one has 5 generations, with the first 3 also having the vertices labeled by Farey fractions.

There is also a slightly higher resolution version on Youtube.

Notes

If you do a stereographic projection of the "Poincare ball" that I made onto the plane, you get patterns related to Schmidt arrangements.
Here is a nice web page by Katherine E. Strange on that.

Notation of Farey fractions.
We can multiply the numerator and the denominator by a factor, and get the same fraction. We like to have a unique notation for a Farey fraction.
We choose the factor so that as many as possible elements of {a,b,c,d} in (a+ib)/(c+id) are non-negative. First we make c and d non-negative. If one of {c,d} is zero, we can make a non-negative. If both are zero, or if a is zero, we can make b zero.

I found 2 articles by Meira Hockman helpful:
The geometry of Gaussian integer continued fractions
The Farey octahedron graph, the Poincaré polyhedron theorem and Gaussian integer continued fractions

Who better to explain the relationship with Monstrous Moonshine than Richard Borcherds himself, who proved the Monstrous Moonshine conjectures.