Laser-cut Pythagoras’ theorem puzzle

Move Website

My website is  moving.  Best go to the  new location at westy31.nl/Pythagoras.html      This old page will be gone soon...


Gerard Westendorp

This page provides some background information on a laser-cut puzzle based on a proof of Pythagoras theorem.

Laser cut Pythagoras Puzzle
The puzzle is based on the fact that you can tessellate the plane using two arbitrary squares a2 and b2 and from this construct a third set of tessellating squares c2, as shown below.
This implies a2 + b2= c2, obviously the area of the plane is independent of how you dissect it.
(This might be a cool idea for your kitchen floor...)

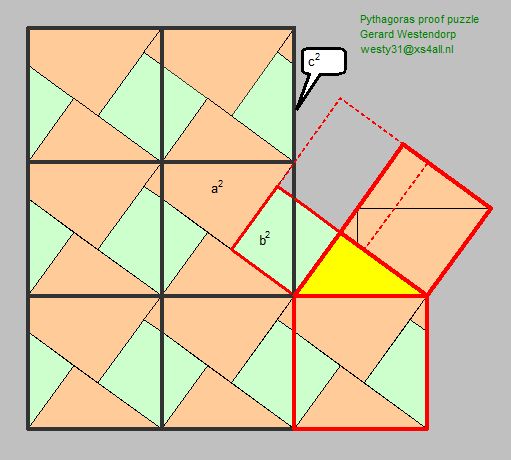
Pythagoras Proof

The puzzle has an a2 square translated so it aligns with a triangle.
To show that this construction works for all {a,b,c}, I made the animation below.

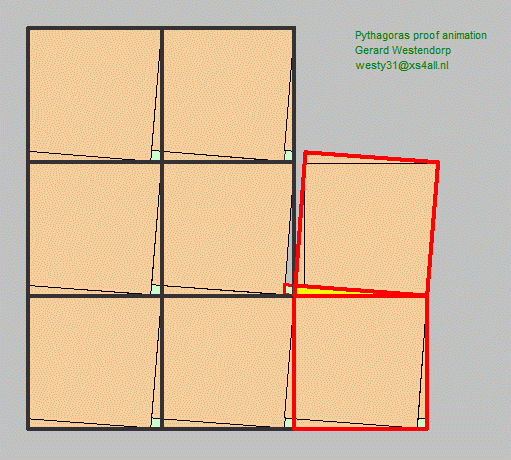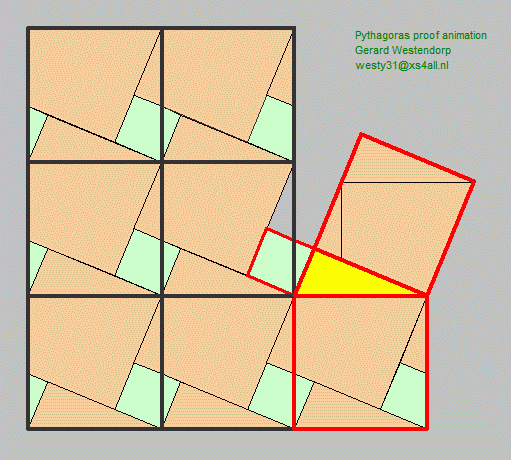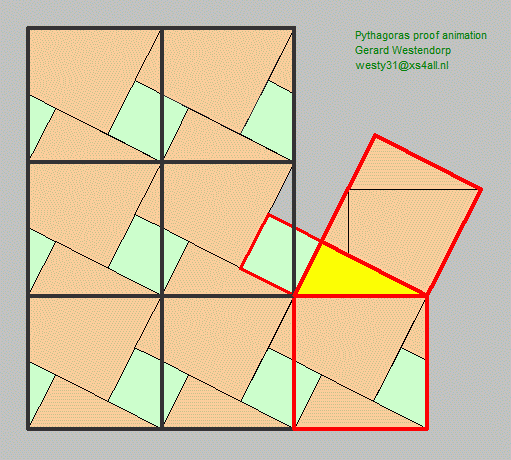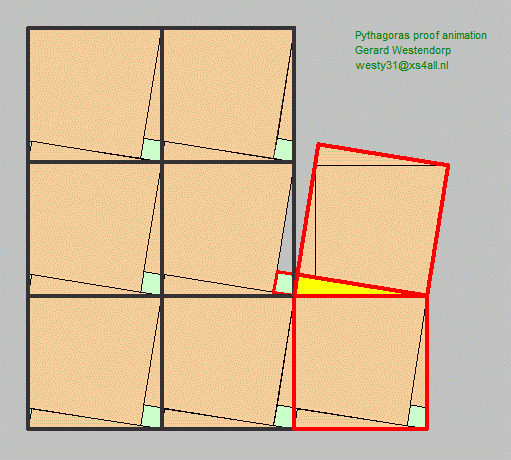
Animation Perigal style
The nice thing about this proof, is that it can be made into a puzzle. The same is true for the more well known proof called as Perigal's proof.
Apparently, Perigal even has this one carved on his tombstone!
I thought Perigal's proof might yield a too easy puzzle, so I used this one.
It turns out to be surprisingly hard. When I first got it from the laser cutting shop, it took my several minutes to solve.

The idea came from a file on Wikimedia commons, here:
[I have not seen the proof used in this anywhere else, so maybe the author of the Wikimedia commons discovered it.]
->Actually, after further Googling, I found that Al-Nayrizi may have discovered it in 900 AD.
I also found out that the tessellation of the plane I used is called a Pythagorean tiling. This Wikipedia page explains how both Perigal and Al-Nayrizi can be constructed from it.

You can buy this puzzle on Etsy.