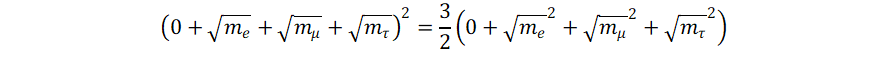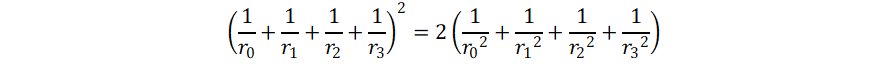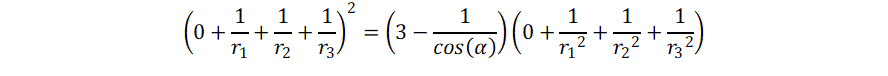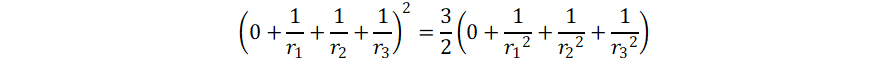The
Koide Formula and the Kiss Precise
 Home
Home
The Koide formula is a strange relation
for the mass of the electron, muon and tauon:
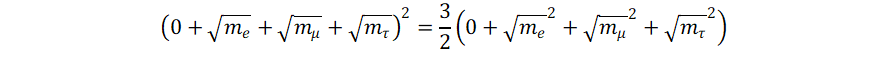
This formula could be pure coincidence. But is holds quite accurately:
I was triggered into this subject by a post
by John Baez on his web log.
It reminded me a bit of the "Kiss precise" formula.
The Kiss precise is a famous formula for the condition under which four
circles exactly touch. It is also known as Descartes theorem. It has
probably been known since ancient times, and rediscovered many times.
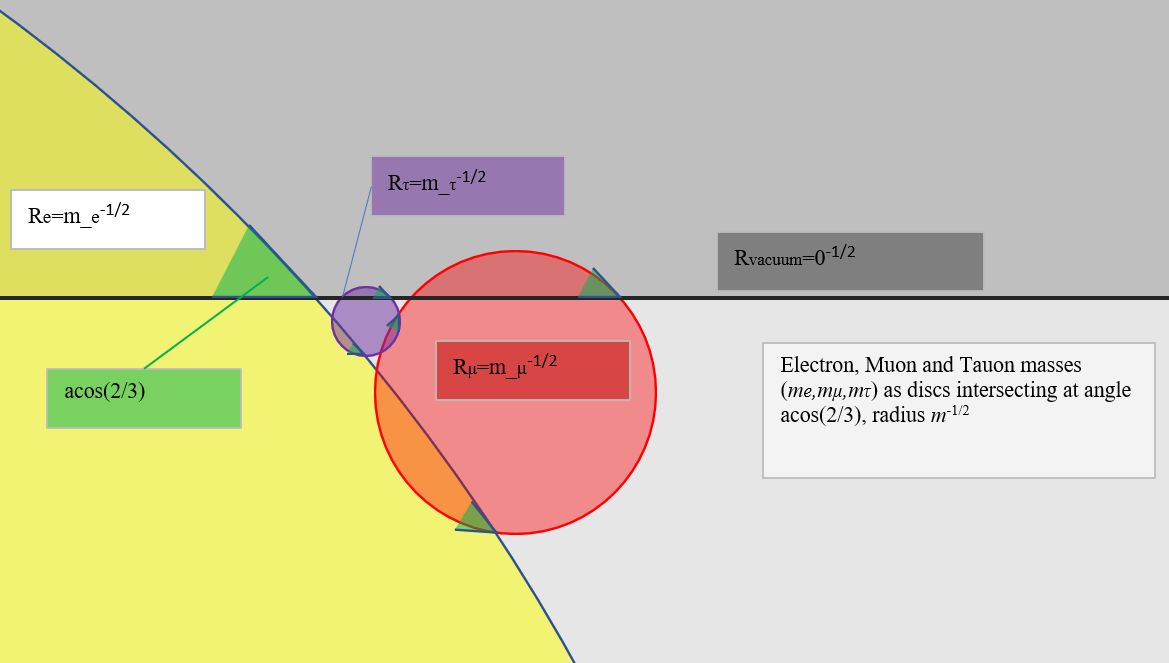
We turn one circle into a straight line, a circle of 1/r=0:
It can be generalized to th case where the circles do not touch, but
intersect at an angle (α).
If 1/cos(α) = 3/2, we get
Now it looks identical to the Koibe formula.
There is a nice proof of
the kiss Precise by Jerzy Kocik,
from which this can be derived,
So we can make the following drawing:
The value of 1/cos(α) = 3/2 is somewhat special, it
is
exactly equal to the ratio it gives for (the square of the
sum) to
(the sum of squares) of the inverse radii.
Here is the poem "Kiss Precise which the chemist Frederick Soddy
published in Nature in 1926:
For
pairs of lips to kiss maybe
Involves no trigonometry.
This not so when four circles kiss
Each one the other three.
To bring this off the four must be
As three in one or one in three.
If one in three, beyond a doubt
Each gets three kisses from without.
If three in one, then is that one
Thrice kissed internally.
Four circles to the kissing come.
The smaller are the benter.
The bend is just the inverse of
The distance form the center.
Though their intrigue left Euclid dumb
There’s now no need for rule of thumb.
Since zero bend’s a dead straight line
And concave bends have minus sign,
The sum of the squares of all four bends
Is half the square of their sum.
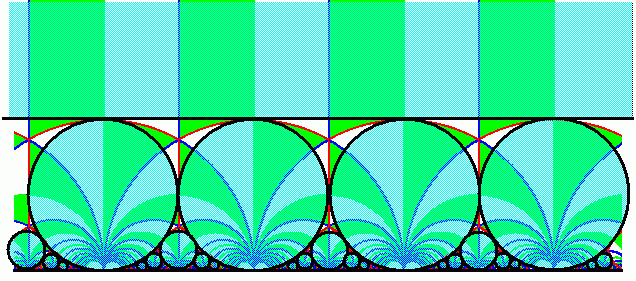
The Kiss precise pops up in many pace throughout mathematics.
For example, here we see touching disks tiling the J-invariant, in the
form of so-called
Ford circles.