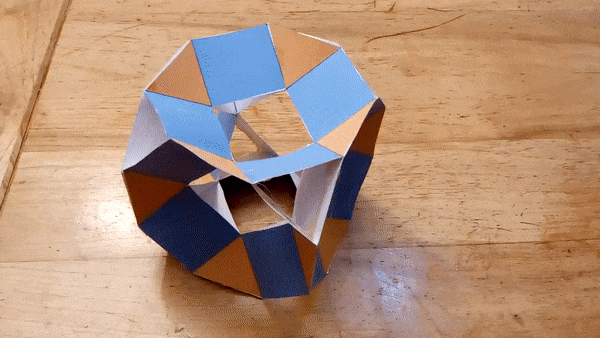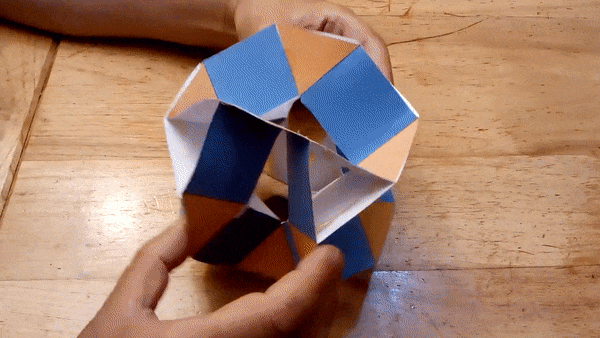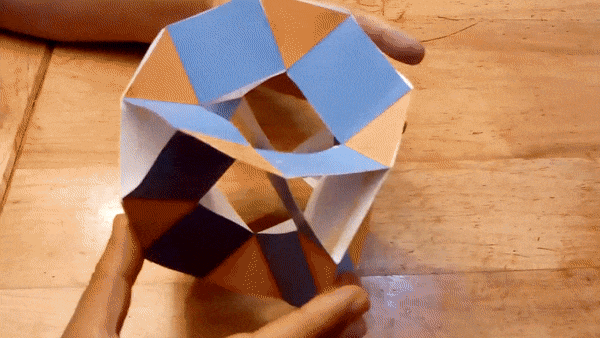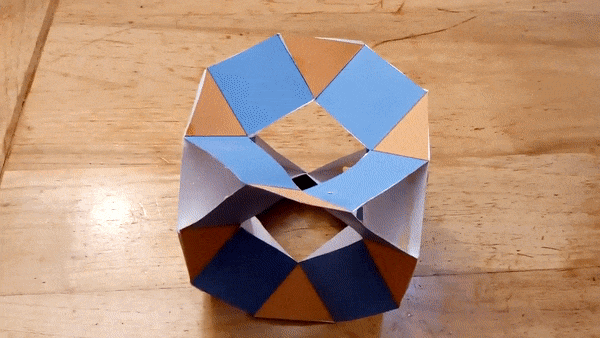Hinged polyhedra and hinged Tessellations
Move Website
My website is  moving.  Best go to the  new location at westy31.nl/Hingedpolyhedra/Hingedpolyhedra.html      This old page will be gone soon...

Gerard Westendorp

I first learned about hinged tessellations from "The Penguin Book of Curious and Interesting Geometry" By David Wells.
This was probably somewhere around 1995.
     Penguin bookFromWolfram2FromWolfram1

I wondered if they could be generalised to polyhedra, and was pleased to find that they could!
I wrote a letter (there was not so much Internet then) to David Wells, including some pictures of the hinged polyhedra I made. David Wells wrote back that he liked this result, and recommended publishing it. I never did that till now, finally, I made this web site.

One cool thing  people missed about hinged tessellations is what happens when you continue the hinge motion past the point when the squares start to overlap.
Surprisingly, the tessellation collapses into a single square. It is actually possible to build this as a mechanical construction, by having each square on a different height, and having hinges that connect between different heights. They do not work full circle, after about 270 degrees, the hinges collide.
Collapsible Tesselation


I built several working physical models. Below is a laser cut model.
Laser cut Square tesselation model(It also in this  video)

Below are the 3 hinged polyhedra I  "discovered". I later found out that the octahedral case was discovered by Buckminster Fuller. He called it the Jitterbug. The other 2, I had not seen anywhere else. Recently I found an article by H.F.Verheyen, that mentions them, along with a lot of other hinge construciton. As time passes, I find more and more people who have rediscoverd these things.
Jitterbug Hinged CuboctahedronHinge IcosaDodecahedron

A nice property of hinged polyhedra is that they transform between several uniform polyhedra.

The octahedral case.
As it transforms from octahedron to cuboctahedron, it goes through the phase of 'snub octahedron', better known as the icosahedron.  So far, this is fairly well known. But now, we progress through the self-intersecting cases, and encounter the great icosahedron! Other phases are compounds of tetrahedra, and coinciding tetrahedra.
 Hinge Octahedron


The cuboctahedral case.
The non-self-intersecting stage is goes from rhombicuboctahedron > snub cube  > cuboctahedron.
The self-intersecting stage includes two coinciding octahedra, and the Great cubicuboctahedron. The intersecting snubs do not seem to be uniform polyhedra.
 Hinged Cuboctahedron


The icosadodecahedral case.
The non-self-intersecting stage is goes from  Rhombicosidodecahedron > Snub dodecahedron > Icosidodecahedron.
The self-intersecting stage includes two coinciding octahedra, and the Great_ditrigonal_icosidodecahedron. On the way also forms a compound of an icosahedron and great dodecahedron. The intersecting snubs are not uniform as far as I can tell.
 
Hinged Icosadodecahedron

I constructed several working models of these hinged polyhedra. Below are the most recent ones, made from laser cut pieces. The hinges can be "snapped" on the polyhedron faces, so the assembly is quick.
Jitterbug modelHinged Cuboctahedron modelHinge Icosadodecahedrom Model

An animation of a 3D printed version:
Animaiton hinged icosidodecahedron

The hinges are printed using a thin layer of PETG.

On Twitter, @HCO28970306 shows all kinds of hinge constructions, using skillful 3D printing technique:

Animation from twitter

Here is a Youtube video Youtube screenshotin which you can see them in action.


Variations

A "meta hinged octahedron
Meta hinge octahedron

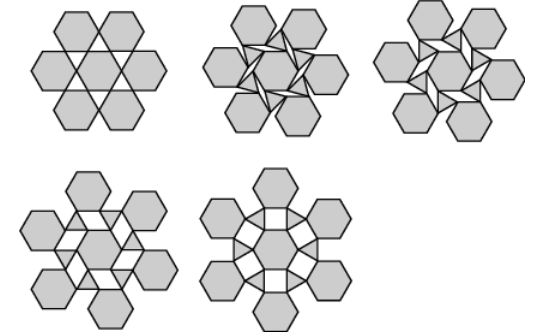
Another planar tessellations.


Hexagonal collapsible tesselation
Al Grant has a nice page on hinged tessellations, with surprising generalisations to irregular ones.
Here is an example:
Al grant's irregular tesselation


Inspired by this, I of course had to make something myself:


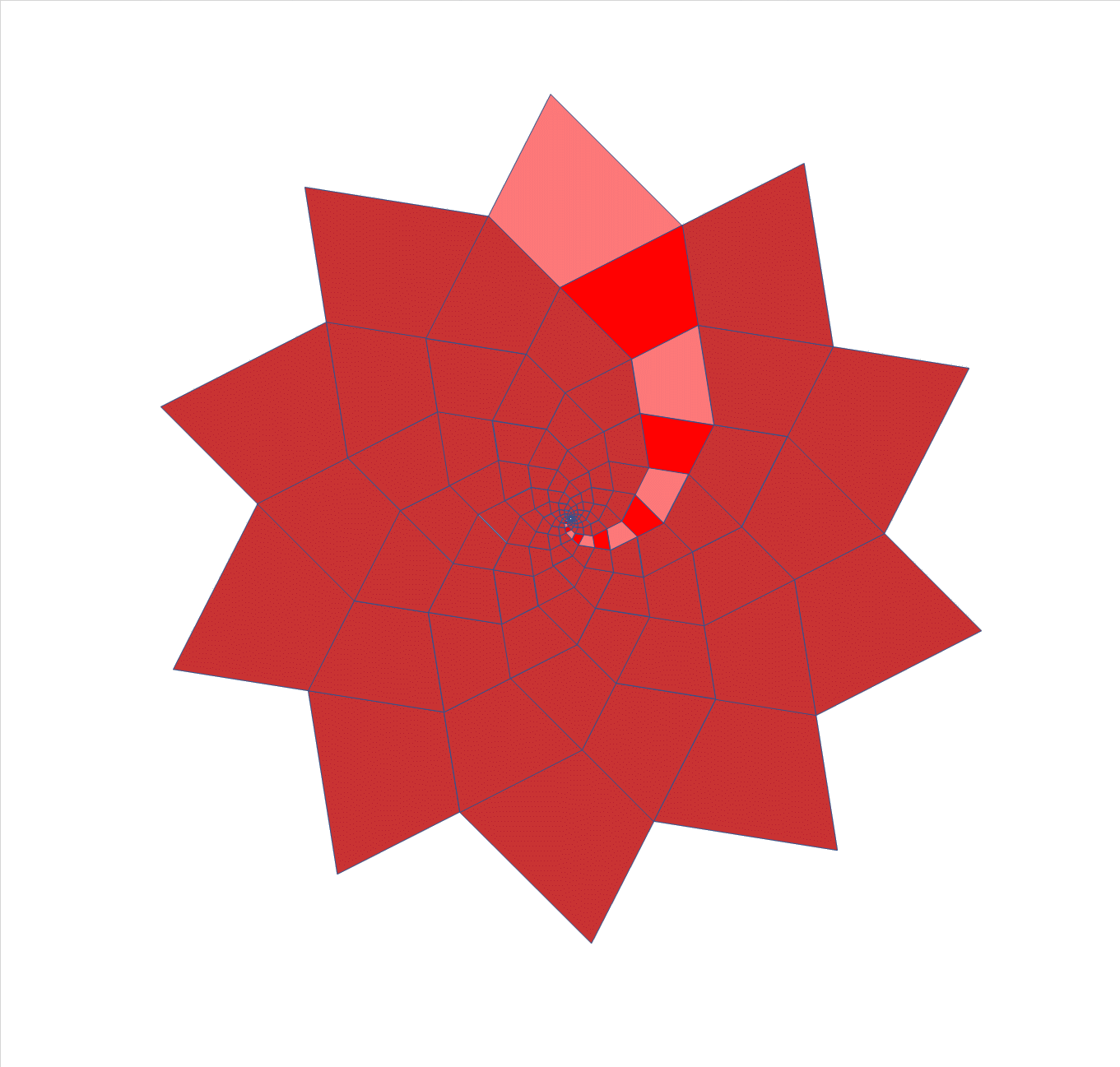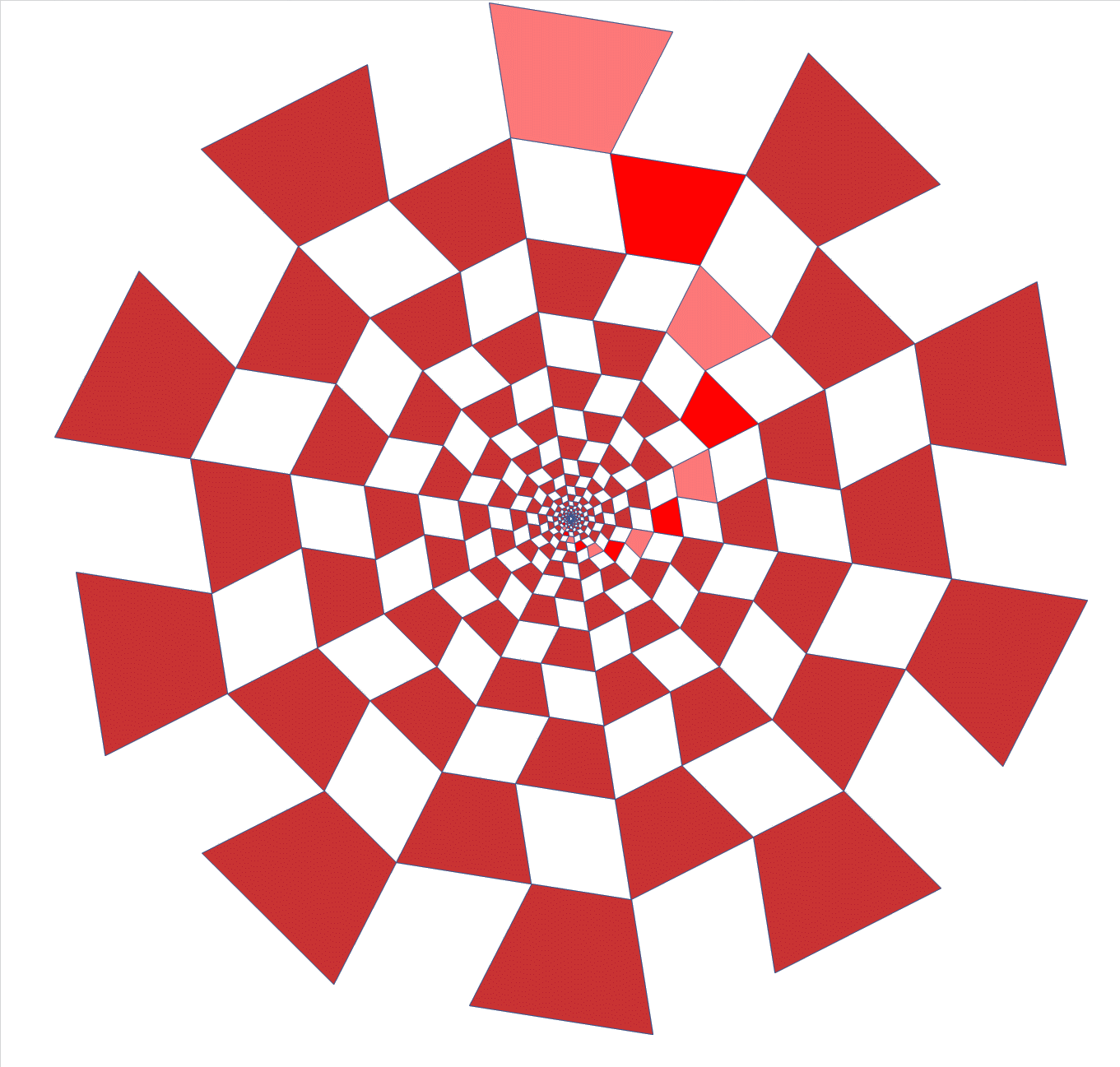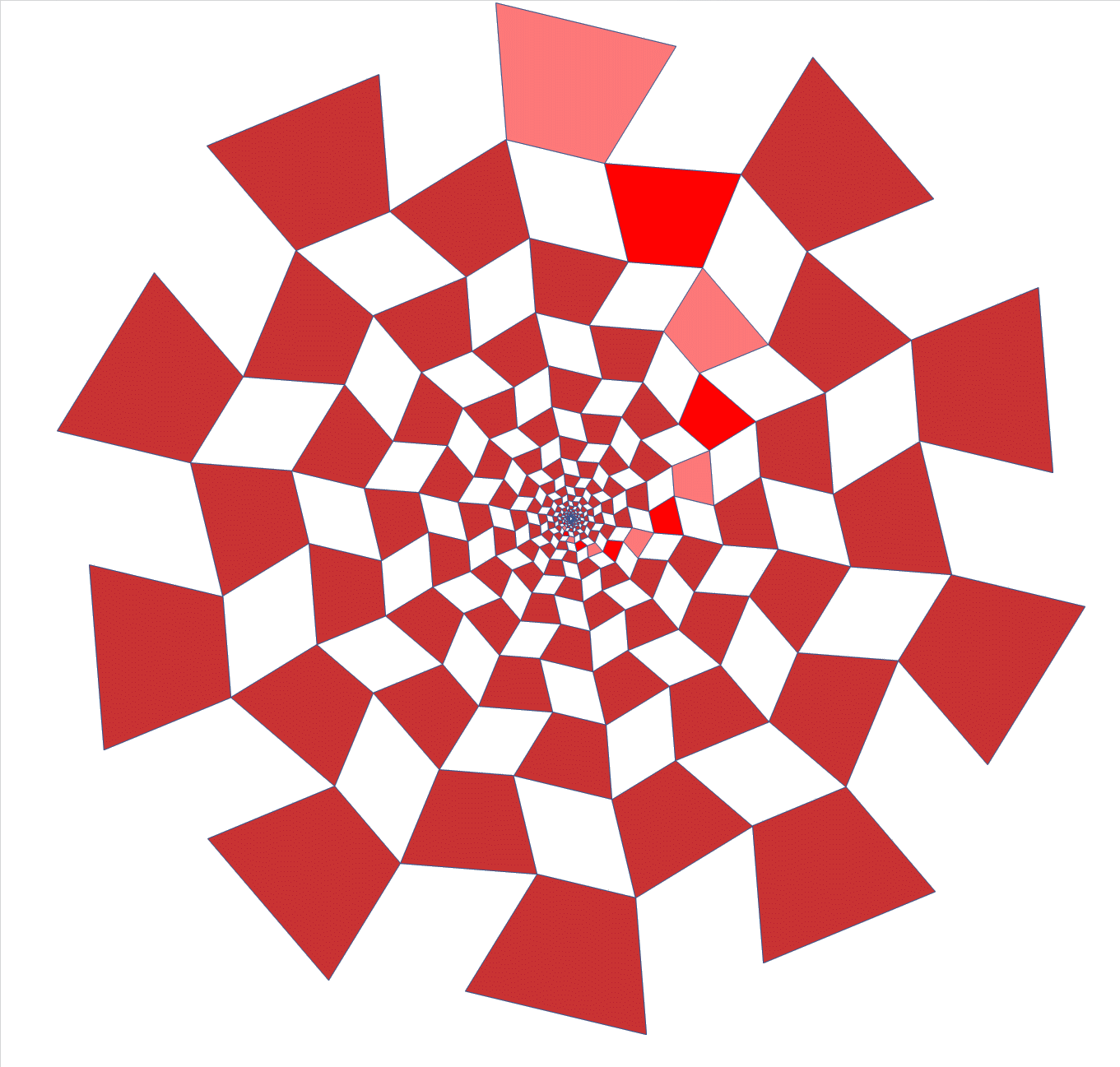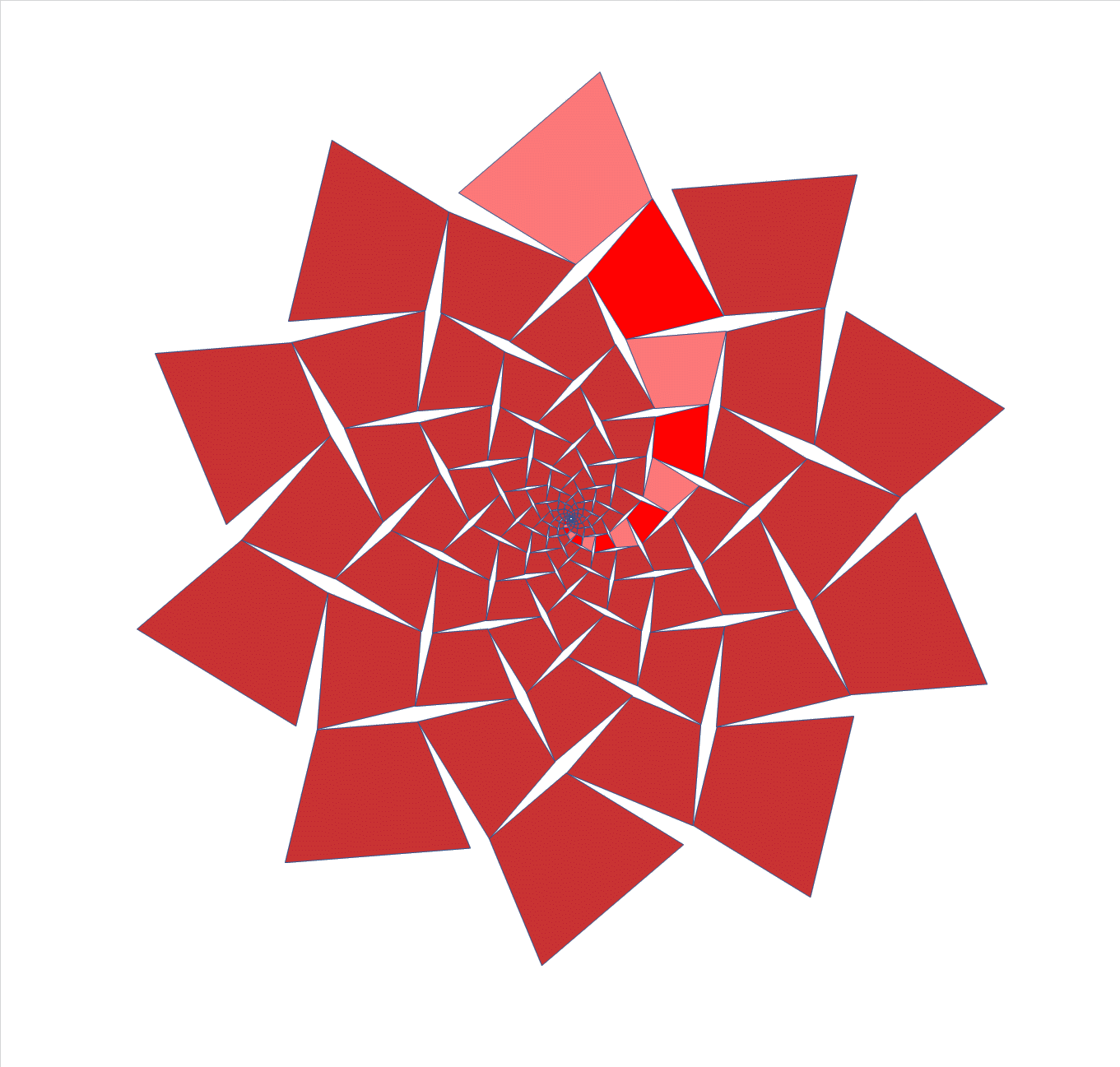
">Hinged Tesselation

A hinged Pythagoras tree

Hinged Pythagoras tree
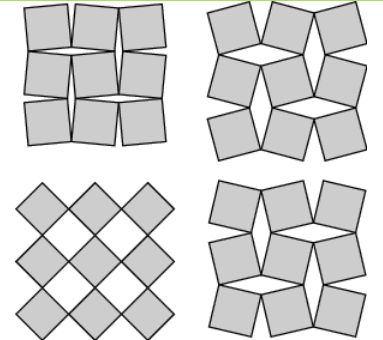
After people remarked on Twitter that any tiling composed of rhombi, can be converted to a hinged tiling (connect the midpoints of each rhombus, they form rectangels that can be hinged) ,@akivaw tweeted that perhaps Penrose tiles can be made hinged. Yes! So I made this example:

Hinged penrose tiling

This one feutures Dudeney's dissection from a triangle to a square:
Hinged tesselation with Dudeney's dissection

Augmented Jitterbugs
If you take a jitterbug, you can put a structure on top of some of its faces, so that you can make a hinged tetrahedron, or a hinged cube:
Hinged Tetrahedron Hinged cube
Or you can extend the hinges and get this tructaded cube:
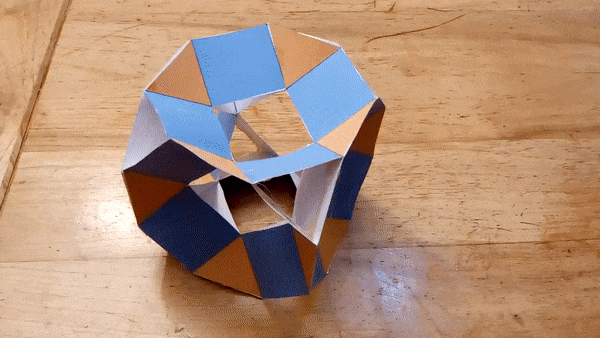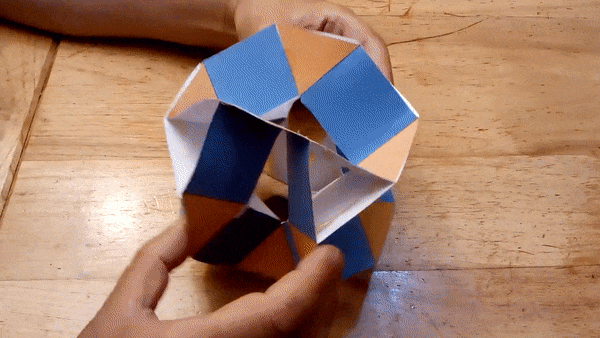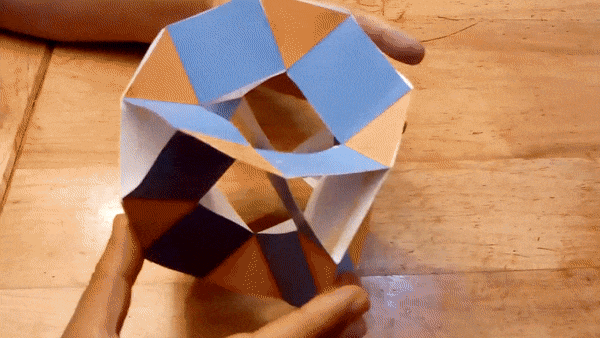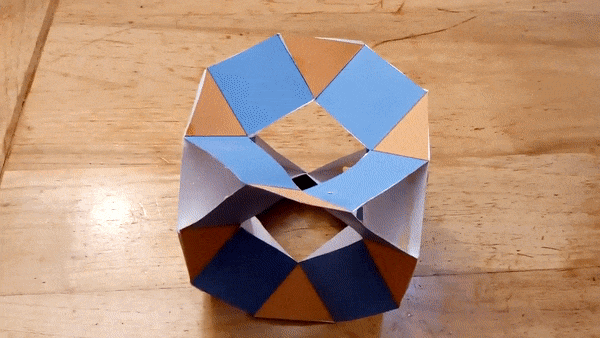
Augmented Jitterbug
On twitter, @KangarooPhysics stretched the 12 hinges and attached attached triangles to them, so that you get a hinged icosahedron!:
Daniel Piker icosa jitterbug

Finally, a tetrahedron that hinges into a gyrobifastigium, one of the 92 Johnson solids.
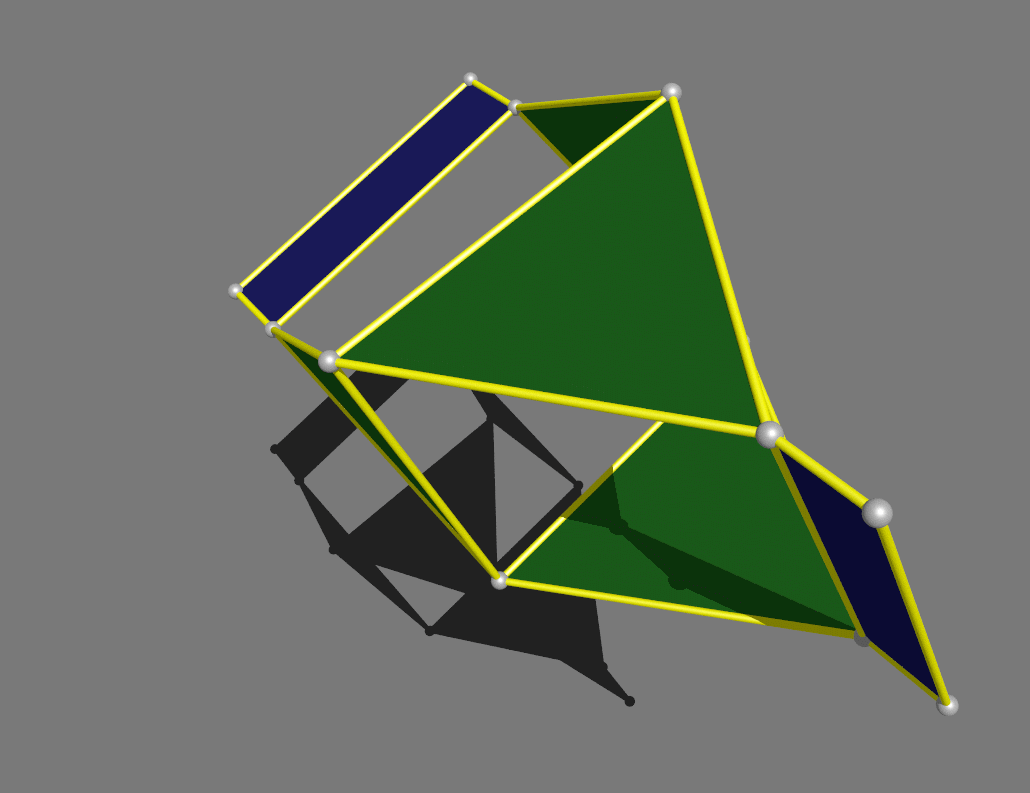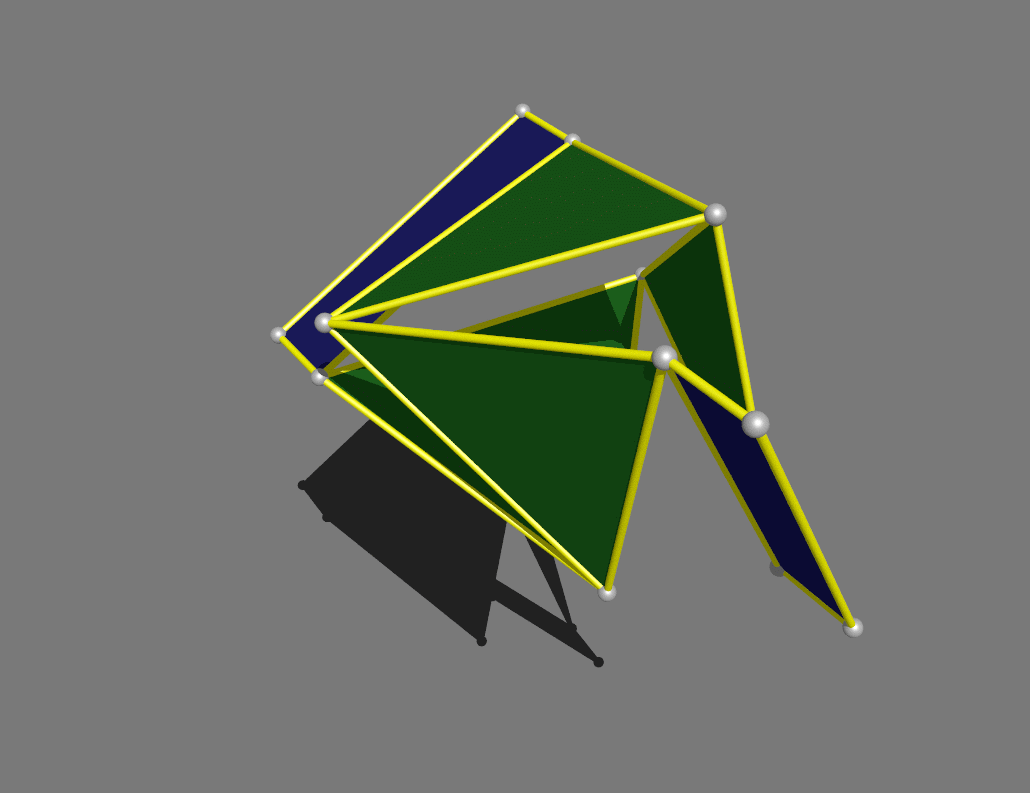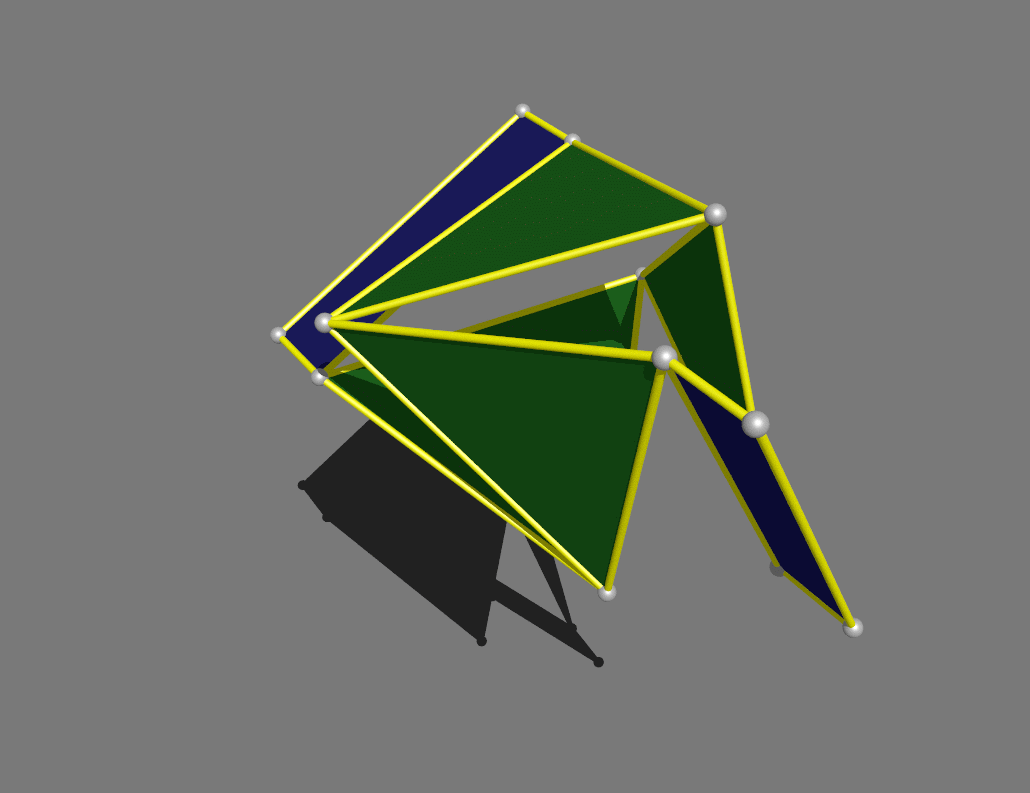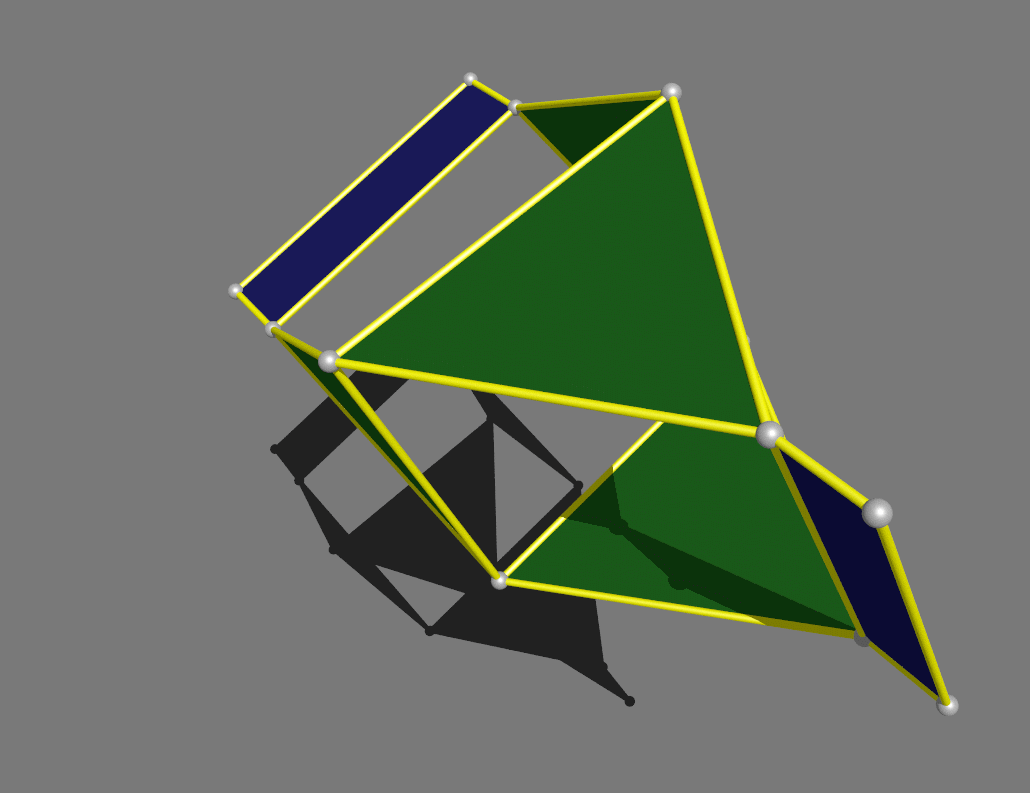
Hinge gyrobifastigium
On Twitter, @HCO28970306 shows a 3D printed model of it.

Gluing together hinged polyhedra.
You can glue together hinged polyhedra to create larger structures, for example cristal lattices. A curious property of such latices they have negative Poisson's ratio: When you stretch them in one direction, they do not, as ordinary materials, contract in the other directions, but expand. This property is called 'auxetic'. Henri Segerman has made a 3D print version of what he called the Jitterbox, Jitterbugs in a lattice. Here is my own example, Glued together hinged cuboctahedra, but addition each square has been sub-divided into a 3X3 collapsible square tessellation. 
 Hyper auxetic hinged construction
The number of possibilities seems to be very large!
Antiprism is an interesting  site, it explores what  the author Adrian Rossiter calls "Chiral Polyhedral Transformations".
These overcome the limitation that on each vertex, you need an even number of faces meeting to construct a hinged polyhedron. For each face, he creates 2 copies, an inner and outer, and the hinge always connects an inner with an outer.  The inner and outer faces move in opposite directions. In this way, you can make a hinged cube (and lots of other variations):
Antiprism's method for overcoming the odd valency probelm
It turns out this construction also simplfies the hinges: The construciotn is stable as long as you keep the hing points together, for example with a simple hook.
Recently people are studying hinged metamaterials, using structures with several internal degrees of freedom, so that
Chuck Hoberman, has created many cool hinged structures.

Here is a Youtube video of a talk I did on hinged polyhedra.

Recently, I learned that a lot of stuff had been going on in the past that I didn't know about.
Here is a video about Ron Resch, who was doing hinged polyhedra in the sixties!
Many of the things I discovered were in fact rediscoveries. The video also shows things completely new to me.
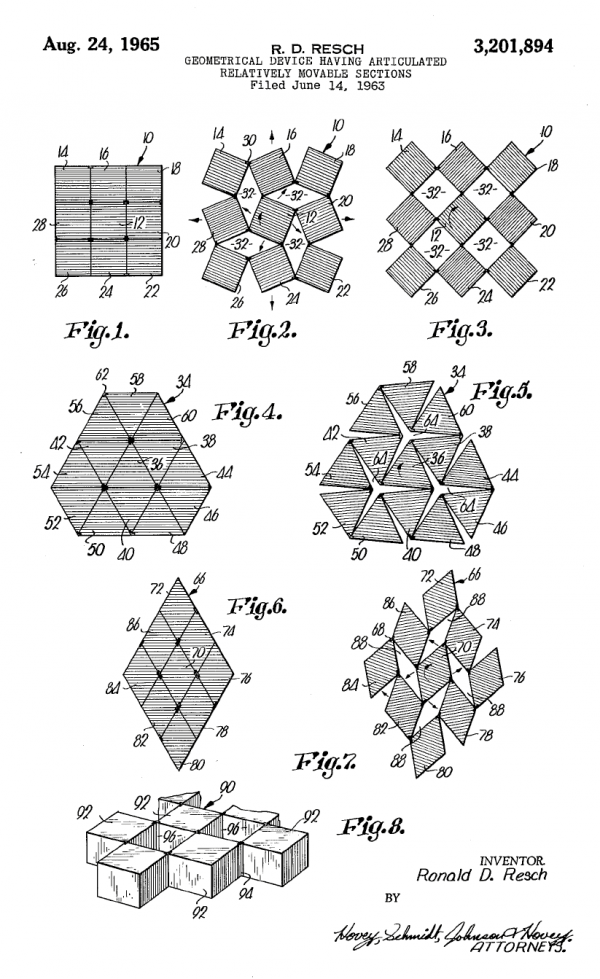
He patented hinged tesselations already in 1964.
Ron Resch  Patent Resch

Here is an animation of a 3D hinged cube array, that generalises the 2D hinged tesselations in a cool way. Ron Resch built large models of this.

Animation Ron Resch cubes

Another person I learned about who was doing things already in the 1960s is Joseph Clinton. 
Joseph Clinton
Here is a video by Joseph Clinton. He beat me by several decades in building some of his models!