Circle packings and ripple points
(Under construction)

In this page,  I discus some aspects of circle packings in more detail than on my main geometry page.

Ripple points
I use the word "Ripple points" for points on a surface that have negative intrinsic curvature, whose coordinates it's neighborhood are smooth functions, but that may nevertheless not qualify as C²

These ripple points can in a region around the origin be described in polar coordinates (R,φ):
   z = R² cos(φ*N)
Below are a couple of plots:



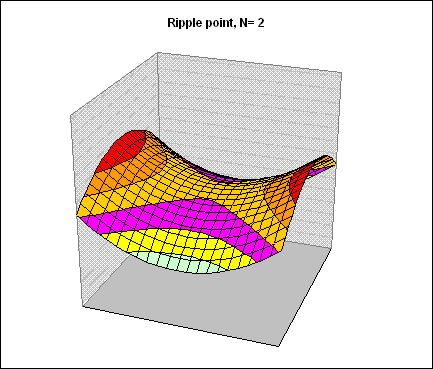
So, the sectional curvature along a line through the origin, with angle (φ) is
   d²z/dR² = 2 cos(φ*N)

If  N = 2, we get a "normal" saddle point, with principle curvature lines  at φ=0,φ=π and = π/2,φ=3π/2.

If N=4, we get more than one set of lines of principle curvature.
So although the z-coordinate is a smooth function along any line in (x,y) though the ripple point, we cannot define the principle lines of curvature, so we do not have a well-defined mean curvature. We could still define a Gaussian curvature, as this is invariant under isometries: we could locally "iron out" the ripple point.

So Ripple points are pretty smooth, but still do not qualify as C²
The point is, that by allowing Ripple points, we can side-step Hilbert's theorem, and create surfaces of constant negative curvature! 

Circle packings

There are a lot of cool pages on the web.
Here are a couple of links
Ken Stephenson Author of a book on circle packings and creator of the program 'Circlepack'
Science news online article about Descartes formula
David Gu
Gallery by Jos Leys
Univerty of Berlin Discrete Geometry Group





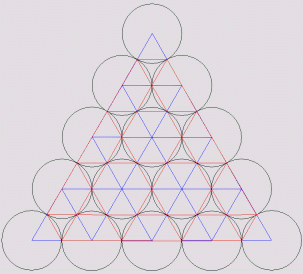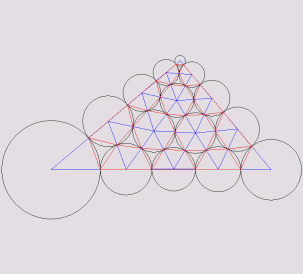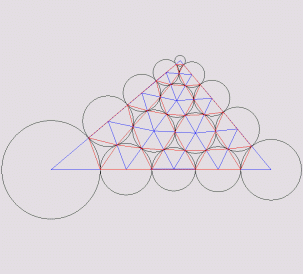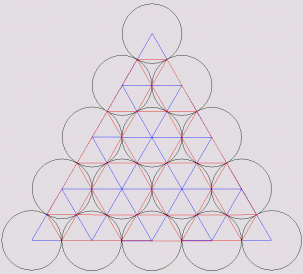
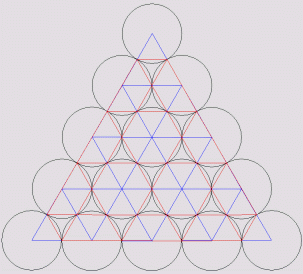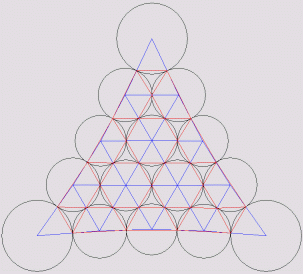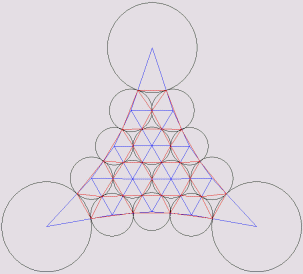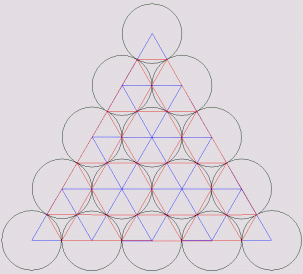
Rendering a packing with spheres.

Once you have computed the coordinates and radii of a packing, you can easilly render it using VRML. Just create an ASCII file, with the extension ".wrl", and your browser will open it in a VRML or X3D viewer. (If not , you need to install an appropriate free plug-in).
A sample ASCII code is shown below. If you open this in a VRML viewer, you would see 2 circles.
The 3 numbers after the word 'translation' are the coordinates of the sphere center.
The  number after the word 'radius' is the radius
The 3 numbers after the word 'diffusecolor' are the RGB values of the color.

#VRML V2.0 utf8
Transform {translation
-0.233475641291208  -0.233475641291208   0.606344887518922 
children [Shape { geometry Sphere { radius  4.74575427128103E-03
} appearance Appearance { material Material { diffuseColor 0 0 0.6
transparency  0.01 }}}]}

Transform {translation
-2.90975547990388E-17  -0.291075073423207   0.601842589785694 
children [Shape { geometry Sphere { radius  4.41228356341674E-02
} appearance Appearance { material Material { diffuseColor 0 0 0.6
transparency  0.01 }}}]}

Another way to render a surface is using the "IndexedFaceSet" node of VRML. You can see how that works by saving a VRML model such as this one, and opening it in a text editor.