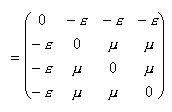Electric
circuit diagram
equivalents of fields
Home
Heat
conduction
Circuits
on an arbitrary triangular
lattice
The
N-simplex equation
Higher
order discretization
Acoustics
Animation of
Acoustic circuit
Navier
Stokes equation
Electrostatics
Maxwell
equation
Animation of Maxwell
circuit
Schrodinger
equation
Space-Time
circuits
Curved
Space time
Klein
Gordon Equation
Dirac
equation
Further
work
Links
Electric circuit diagrams were originally intended to be purely
practical
drawings, showing how to build a circuit from components. This remains
their
most important application, but they also turn out to be very general
representations
of mathematical and physical systems. Apart from actual electrical
circuits
they can describe things as diverse thermal conduction, acoustics,
quantum
mechanics, algebraic equations, differential equations and topology. As
someone
once said: "All sufficiently beautiful things are deeply
related to
all other beautiful things." So are circuit equivalents sufficiently
beautiful?
In this article, we apply circuit equivalents to fields. Fields
are normally treated as continuous systems. The way to treat continua
is
to discretize them in such a way that you can refine the discretisation
as
many times as you want. Then you say that in the limit of refining an
infinite
number of times, the discrete system becomes indistinguishable from the
continuous
system. It turns out that you can do that with circuit diagram
equivalents
of fields.
Electric circuit equivalents of fields are not mere
approximations of continuous fields, they can be viewed as being
physical
systems in their own right.
Analogies
In each case in this article, we draw up a circuit, and then show that
it is "equivalent" or "analogous" or isomorphic to some phenomenon or
system. This means that for each electric
quantity in the circuit, there is a corresponding quantity in the other
system
and vice versa. So after we filled in for example "Temperature" for
"Voltage",
we can treat the system using the machinery of circuit theory.
The
principle of Minimum Dissipation
In principle, we can do all
circuit analyses with just
voltages and impedances. But sometimes it can be handy to introduce
extra concepts, and here we want to introduce the concept of the
generating functional. (A functional is a formula that produces a
number from a set of variables.) The main motivation
for this is that in contemporary theoretical physics, the "Principle of
Least
Action" is considered to be very important. I want to see how this is
related
to circuit equivalents.
First we will derive an
expression for the dissipation in a
circuit, and see that the total dissipation is a funky functional.
The set of i
equations for a circuit with i
vertices:
∑ j
(Vj
- Vi)/Rij
= 0
By multiplying this by 2Vi
,
and summing over all i,
juggling a bit with
indices, we get:
∑i,j
(Vj
- Vi)2
/Rij
= 0
The term (Vj
- Vi)2
/Rij
will be recognized as
the dissipation by the resistor Rij
The theorem we just derived says that the
total dissipation
in a circuit is zero . We can
also see that if Voltage is a
real number, and resistance is a positive real number, as is the case
for "ordinary" circuits, then the dissipation in each component is
positive. This implies that the only solution to a circuit without
sources of energy is that all currents and all voltages are zero. So to
do anything interesting, we have to put in some sources, or consider
putting in as negative or imaginary resistance somewhere.
 A cool property of the total dissipation is that you can recover all
equations
for the circuit by requiring that the total dissipation is in a minimum
with
respect to small variations of
Vi
. Mathematically, this is saying all derivatives to Vi
are zero:
A cool property of the total dissipation is that you can recover all
equations
for the circuit by requiring that the total dissipation is in a minimum
with
respect to small variations of
Vi
. Mathematically, this is saying all derivatives to Vi
are zero:
d/dVi
{ [ ∑i,j
( Vj-Vi
)2
/Rij
] }
= 2 ∑
j
( Vj-Vi
)/ Rij
= 0
Which is the original set of
equations.
This is why the total dissipation can be considered the generating
functional
of the circuit. Deriving the equations from a generating functional is
not
really adding any new physics, but it is especially useful in seeing
how
different ways of describing things are equivalent.
We call this trick the
principle of minimum dissipation
. It has interesting analogs for the different kinds of circuits I will
discus. For instance in one case it maps onto the  principle
of least Action . The principle
of least Action is considered
by some to be the most fundamental principle in theoretical
physics.
principle
of least Action . The principle
of least Action is considered
by some to be the most fundamental principle in theoretical
physics.
The "principle of minimum
dissipation" is really a catchy but
oversimplifying phrase. It is more accurate to say that
all derivatives of the functional with respect to certain
state variables
are zero. For example, if we had said:
S
= ∑i,j
Iij2Rij
and then minimize dissipation
by varying Iij
instead of Vi,
we would have
obtained:
Iij
= 0
But these equations are a bit boring, they do not reflect the structure
of the circuit. Moreover, they cease to be true as soon as we put in
some
source, so that Iij ≠
0 In order to use the generating functional for generating the circuit
equations we need to express it in terms of Vi.
The reason that a minimum in Vi
is not necessarily a minimum in Iij
is that the space of Iij
generally has a different number of degrees of freedom than the space
of Vi.
k-chunks
Dissipation is an example of what I call an k-chunk.
All quantities
on a circuit represent a finite piece of "something", or a "chunk". An k-chunk
is a quantity that scales with lengthk
.
0-chunks, also known as
intensity variables , are
quantities that (approximately) do not change if you refine the
discretisation.
Examples are Voltage, Temperature and Pressure. In N-dimensional
space, N-chunks
correspond to extensity
variables , they scale with
volume. Examples are mass,
charge, energy, dissipation.
Differential geometrists would talk about (N-k)-forms.
A k-chunk
is an (N-k)-form
integrated over an k-dimensional
subspace.
A voltage difference across an edge is a 1-chunk. In N-dimensional
space, the current through an edge is a (N-1)-chunk.
(actually, a "twisted
" (N-1)
chunk, as we will see later) The product of
current and ΔV
is a N-chunk
of the dissipation. This is typical of all circuit analogs: 2
quantities
defined on a component multiply together to form a chunk of the
generating
functional. These 2 quantities are each others dual.
(ΔVoltage/current, ΔTemperature/ Thermal power,
ΔPressure /Volume velocity, etc.). Also typical is that Ohm's
law converts between the 2 sides
of this duality.
Electric
circuit equivalent of heat
conduction.
Set up the analogy
:
V(Voltage)
<-> T
(Temperature)
Q
(Charge) <-> U
(Energy)
I (Electric
current) <-> W
(Thermal Power)
P
(Electrical dissipation)
<-> W
ΔT
(see note)
C
<-> ρCp
ΔVolume
(Thermal capacitance of volume
element)
R
(Electrical resistance) <->
Δs2
/(
λ ΔVolume)
(Thermal resistance)
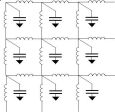
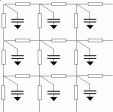
And draw the following circuit :
Figure
1: Electric circuit
equivalent for time dependent heat
conduction.
Applying Kirchhoff's
current law :
dT/dt
= -1/(ρCp)
div (w)  dTi/dt
= -1/Ci
∑j
Wij
dTi/dt
= -1/Ci
∑j
Wij
Applying Ohm's
law :
w
= -(1/λ)
grad
(T) Wij
= -(Ti-Tj)/Rij
Wij
= -(Ti-Tj)/Rij
Combining:
dT/dt
= λ/(ρCp)∇2T dTi/dt
= 1/Ci
∑j(Ti-Tj)/Rij
dTi/dt
= 1/Ci
∑j(Ti-Tj)/Rij
Which is the equation for
instationary heat
conduction.
Note
on irreversibility and the generating functional:
The generating functional
of this circuit is:
S
=
∑edges
(ΔT2
/ R)
+ ∑ Vertices
(d/dt
½
C
T2
)
= ∑edges
(W
ΔT)
+ ∑
Vertices (
T dU/dt)
This quantity looks a bit unfamiliar. We know that it should have
something
to do with irreversibility, because it is the analog of electrical
dissipation,
the irreversible conversion of electrical energy into heat. It would be
nicer
if the generating functional were Entropy generation.
Actually, we can do this by
switching from Temperature (T)
to a quantity that Zemansky called Negcitemp
(N=-1/T).
According to Zemansky (writer of well known thermodynamics textbooks),
it sometimes makes sense to use Negcitemp (Negative
Reci
procal Temperature)
instead of temperature. For small temperature deviations around
a nominal temperature, Negcitemp is just like a rescaled temperature.
For
larger deviations, things get non-linear, but
Cp
and λ
are non-linear functions of T
anyway. So let us assume that
Cp
and λ are
linear in Negcitemp, and get
for the generating functional:
S
=
∑edgesWΔN
+ ∑Vertices
N
dU/dt
= -∑edges
W Δ(1/T)
- ∑Vertices
(1/T)
dU/dt
= -d/dt
(Entropy)
 So now we have the more familiar quantity of entropy generation rate as
the
generating functional, and indicator of irreversibility. This is no big
deal
in practice, but nice philosophically.
So now we have the more familiar quantity of entropy generation rate as
the
generating functional, and indicator of irreversibility. This is no big
deal
in practice, but nice philosophically.
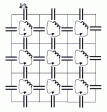
Circuits
on an arbitrary triangular lattice
In most of the circuits in this article, the components are
all placed on a regularly spaced hypercubical lattice. This is
has many advantages, the most important being that I didn't until
recently
know how to do it otherwise.
In a correspondence with Han
de Bruijn , I learned how to
optimally approximate a
continuous system with a lattice composed of arbitrary triangles (or N-simplexes
for higher dimensions).
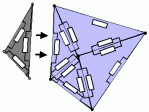
Suppose for the moment that we know
how to do 1 triangle. We can then "click" them
together, combining the parallel resistors on each edge into a single
one,
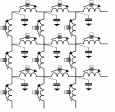
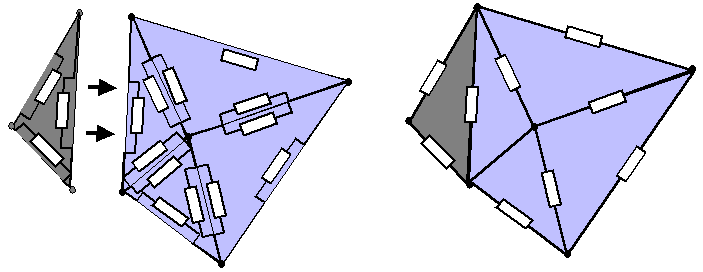
as shown below:
"Clicking
together" a circuit
composed of elementary triangles
of arbitrary shape.
Next, we need to know what resistance values to implement on the edges
of a triangle (ABC):
The
resistance on the edge AB
for a triangle ABC is the same
as that of
a rectangle ABDF. For a right-angled triangle this resistance becomes
infinite
(its cross section is zero), and for an obtuse triangle it becomes
negative.
It turns out that the resistor value is that of a rectangle ABDF
whose length is the same as the edge, and whose width extends from the
edge
to the point (E), the circumcenter
of the triangle. (We will derive
it further on) The
circumcenter is also the point touching
all Voronoi cells of the 3 vertices. In one of his articles
, Han de Bruijn shows that this choice of resistor value gives a model
that
is equivalent to a finite element method. He also shows how this is
related
to finite difference methods, finite volume methods, and some nice
geometrical
properties of triangles.
 Note that for a right-angled triangle, the "hypotenuse" resistor
becomes
infinite. This means that if we click together 2 right-angled triangles
into
a square, as below, we will retrieve the square schemes as we use in
the
rest of this article.
Note that for a right-angled triangle, the "hypotenuse" resistor
becomes
infinite. This means that if we click together 2 right-angled triangles
into
a square, as below, we will retrieve the square schemes as we use in
the
rest of this article.
2
right-angled triangles
combine to give a square, with the
resistor on the diagonal disappearing because it is infinite.
Note also that for obtuse triangles, resistor values become negative.
The
N-simplex
equation.
The relationship between electric circuits, space, and triangulation is
very interesting. It will lead to a model of General Relativity based
on circuits, and to a coordinate free discretisation of fluid dynamics.
So we will talk about it in more detail. After quite a bit of Math, the
outcome will be a compact formula that I call the "N-simplex
equation".
We need general expressions for the circuit equivalent of a
simplex-shaped chunk of continuous space. Let’s derive the
formula for a resistor value in a 3
dimensional
tetrahedron. The generalisation to N-dimensions
turn out to be
straightforward.
We demand that the dissipation (S)
for a circuit of a tetrahedron is
the same as the dissipation for a continuous tetrahedral chunk of
continuous medium, subjected to a current density of arbitrary
direction.
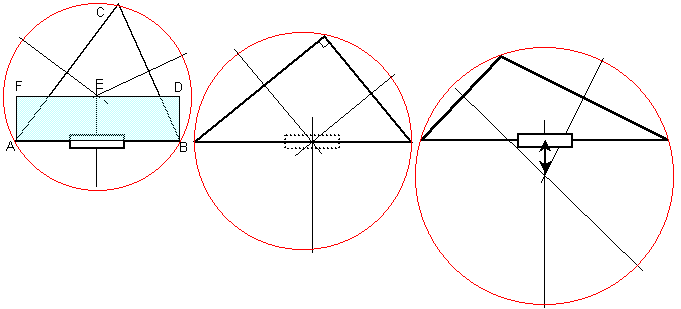
2D
illustration for the derivation of the N-simplex relations.
We know, writing out the circuit equations, the total dissipation (S)
of the discrete network, as a function of the voltages at the vertices
(V0,V1,V2,V3):
Next, we need to find out what the dissipation is in the continuous
case. The simplex is subjected to a current density (i)
of arbitrary
direction. Assuming unit specific resistivity (σ)
for convenience, we
have the voltages differences:
The matrix A
happens to be
just the matrix that transforms a “standard
orthogonal”
tetrahedron to the arbitrary tetrahedron that we are considering.
We’ll
be needing that to see how resistors are related to the metric tensor,
which plays an essential role in relativity.
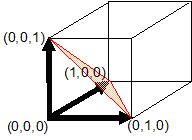
A
“standard
orthogonal” tetrahedron
The matrix can also be used to calculate the volume:
To express the current density as a function of the voltages, we use
the inverse of (A):
We used the fact that the elements of the inverse are related to the
partial derivatives of the determinant to the elements, with
Δ=
det(A):
Now that we can express the currents in terms of voltages, we have the
required expression for the continuous case dissipation, also as a
function of voltages:
Equating the discrete and continuous expressions for S,
we can get the resistance values from the
matrix elements of (AAT)-1.
A very satisfying result is that the matrix (AAT)
is
just the metric
tensor (guv)
of a chunk of Euclidean
space spanned by the
vectors emanating from vertex 0.
So:  There is a 1-to 1 correspondence between
the metric tensor and the
resistor values for each tetrahedron!
There is a 1-to 1 correspondence between
the metric tensor and the
resistor values for each tetrahedron!
To get a more symmetrical expression, in which all 4 vertices
are
equal, we write for the discrete case:
This matrix has determinant zero, so it cannot be directly an
inverse of another matrix. Undeterred, we start of like this:
Here,
V00
is
the potential at the origin.
The matrix (B)
is again known
for computing the volume:
Generalisation to N
dimensions, with determinant (Δ):
Taking the inverse of B,
and discarding the top row, since we want only the current, thus
ignoring V00:
We have a non-square matrix for i
as a function of V,
but for
the dissipation we end up with a square matrix again:
After comparing the matrix elements of the discrete and
continuous case,
we obtain the expression for a single resistor:
This formula is valid in any dimension.
We can
interpret the term as 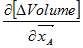 as
a pseudovector (A*)
whose direction is normal to the (N-1)
simplex built from all vertices except (A)
and whose magnitude |A*|
is
the (N-1)
volume, multiplied by a factor 1/N!.
as
a pseudovector (A*)
whose direction is normal to the (N-1)
simplex built from all vertices except (A)
and whose magnitude |A*|
is
the (N-1)
volume, multiplied by a factor 1/N!.
But there is an even nicer formula for the resistor values. For
that, we will need the Cayley-Menger
determinant, which expresses the
volume
of a N-simplex
as a function of squared distances (Lij2)
only (written out for N=3
here) :
The Cayley-Menger determinant leads directly to another famous
expression called Heron’s
formula. But for us the key
feature is an
amazing formula:

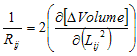 The
N-simplex equation.
The
N-simplex equation.
To derive
it, we refer to the picture below, again using 3D, but
implying generalisation to other dimensions.
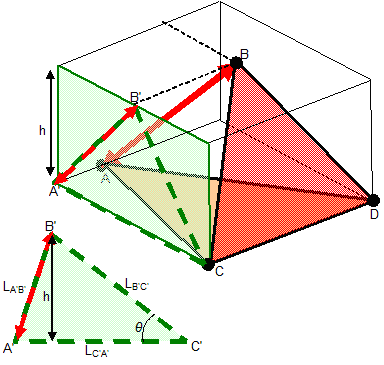
Illustration for the
derivation of the N-simplex relation.
We will use a
projection of the N-simplex
on a plane spanned by the normal pseudovectors A*
and B*.
We
are considering a change in the squared length 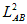 ,
while
keeping all other lengths constant. This means that the shape of the 2 (N-1)
simplices A*
and B*
cannot change,
and the motion of A and B will be parallel to our projection plane. We
split
the squared length (
,
while
keeping all other lengths constant. This means that the shape of the 2 (N-1)
simplices A*
and B*
cannot change,
and the motion of A and B will be parallel to our projection plane. We
split
the squared length (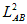 )
into a component in the projection plane (
)
into a component in the projection plane (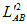 )
and a
component orthogonal to it (
)
and a
component orthogonal to it (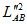 ):
):
We
can now simplify our computations to operations in the projection
plane:
We expand the
volume into a base |B*|
and height (hb),
and
relate this to the angle (θ):
Write (∂hb
/∂θ)
in terms of A*
and B*:
To rewrite (∂θ
/∂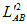 ),
we use the cosine law:
),
we use the cosine law:
Combining, and making
use of  :
:
Finally, we
reach QED:
The N-simplex
equation allows us to get the
resistance values from the inverse Cayley Menger matrix:
Wondering about the mysterious parameters in the top row and first
column? So was I, and I finally figured it out. The answer is
related to the circumsphere, as explained in this article.
One of the cool things about the N-simplex
relation is that
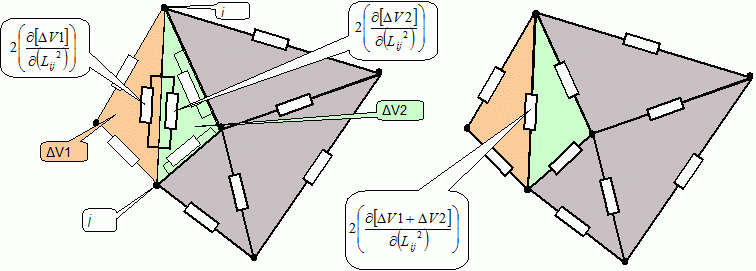
the
Volume in the equation can refer to both the volume
of the
simplex as
the volume as to the total volume of the whole manifold!
This is
because merging resistors on the same edge works the same way as adding
the volumes on each side of the edge. The N-simplex
equation continues
to work.
Volumes that are not connected
to the edge ij,
are not
altered when it varies in length, so we can just look at the derivative
of the total manifold volume. Thus, the N-simplex
equation is similar
to a
functional equation like the principle of least dissipation and least
action.
This idea leads to a nice interpretation of the N-simplex
equation. Imagine the resistors as springs, trying to mininise their
length, while the enclosed volume tries to maximise itself, it is like
a balloon. The equilibrium corresponds to the correct relation between
the resistors and triangle sizes.
Connecting
the vertices with springs with spring constants 1/Rij,
while
trying to maximise the volume of the manifold, produces triangles of
the correct size.
To see this, write out a
generating functional (S),
(interpreted as "elastic
energy" here) which needs to be minimised with respect to Lij
We put in the specific conductivity (σ) explicitly this time,
because it is interesting that this corresponds to the "energy ratio"
between the volume and the length.
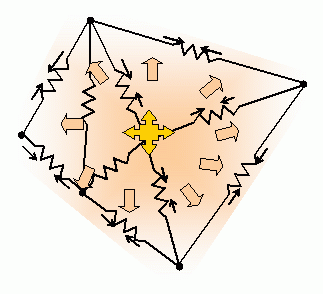
Some 2 dimensional results.
Some interesting expressions for
the
resistors in 2D are highlighted.
Diagram to
illustrate 2D resistor formula.
Combining with the sine
law, we get
Ra =
2 tan(A)
This equation shows a direct relation between the angles of a
triangle, and its resistances. The 3 angles of a triangle in flat space
add up to 180 degrees. This means that the resistors cannot be chosen
independently, if they are to represent a flat triangle.
For a triangle, the circumcircle
radius is given by
This gives the previously mentioned result that
Which can be interpreted so that the resistor is a
rectangular
strip with a
as "effective
length" and ha
, the distance to the
circumcentre. as
"effective diameter". This formula has an interesting consequence for
resistor values of a polygon that lies on a circle.
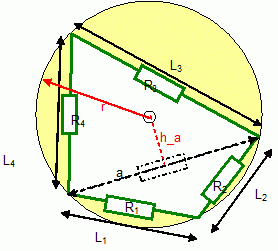
Any
polygon inscribed in a circle has resistor values Ri=Li/(r
2-(
Li/2)
2)
1/2.
A polygon inscribed in a circle, can be sliced into triangles that
share a common circumcircle. An edge that separates 2 such triangles,
with length a,
will have as
distance to the circumcentre for the 2 triangles the value ha
and -ha
respectively. Thus, the resistor
values of these edges cancel precisely. What is left, are only
resistors on the polygon. These have the values Li/(r2-(Li/2)2)1/2.
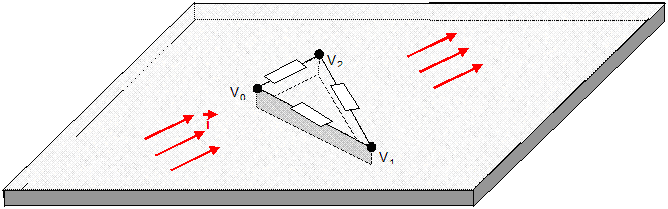
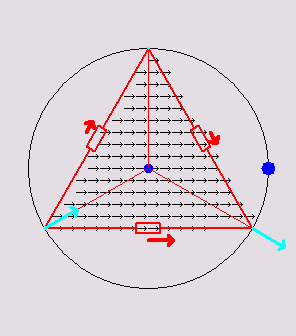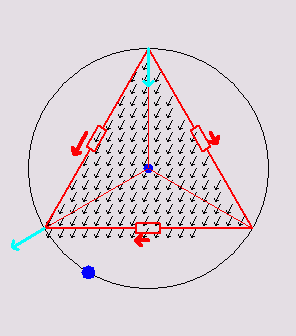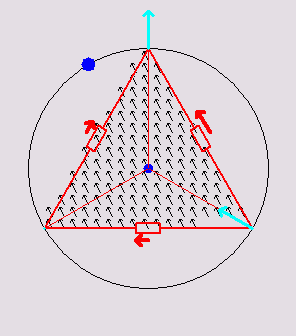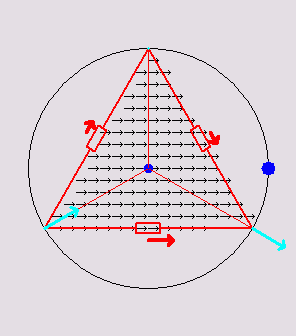
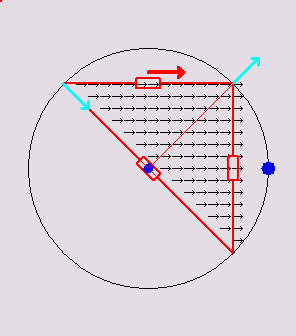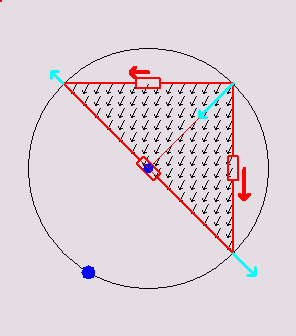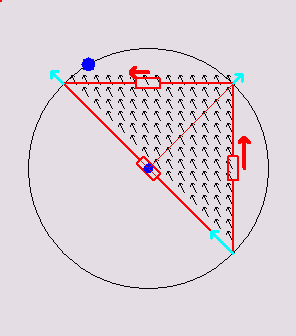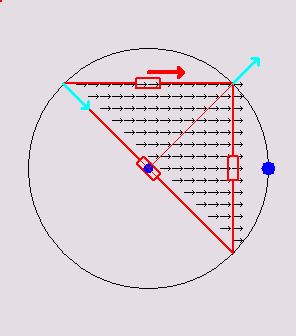
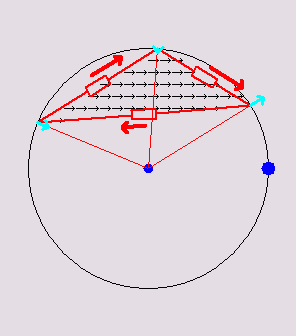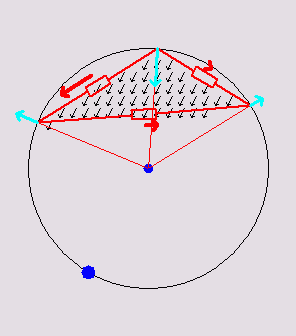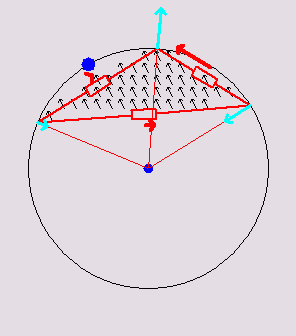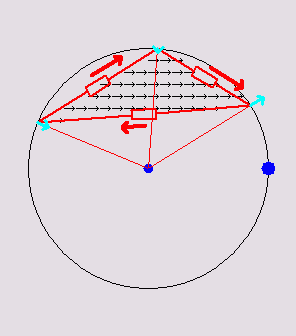
Below are 3
animations that illustrate how a 2D discrete network mimics a
continuous
triangle:
Triangular
circuits
inscribed in
their respective circumcircles. Inside the triangle, a current density
flux of variable direction is animated. The voltage at each vertex is
the same as the voltage of the continuous triangle at those points. The
red arrows show the currents in the discrete
resistors. The total dissipation in the discrete resistors is always
the same as
the total dissipation in the continuous triangle due to the continuous
flux. The cyan-colored arrows depict the net current at each vertex. It
happens to be always equal to 1/2 the continuous flux passing through
the edge opposite to the vertex.
Some remarks on 3D
triangulations
Higher dimensions are trickier than 2D, because splitting up things is
trickier. Below left is a cube split up into 5 tetrahedral
by slicing off 4 corners of a cube You are then left with a 5th central
tetrahedron, which is regular. On the right is another way of slicing
up a cube, this time into 6 congruent ones.
You can assemble the above chopped up cubes into a cubical lattice. The
one of the right yields a cubical lattice in which all
diagonal
resistors cancel, but the one on the left does not. A unit cube
discretized as on the right, gives resistor values of 6 on
each
leg that has one tetrahedral edge, and value 3 for those that have 2
tetrahedral edges. I was puzzled by this at first, but if you look
carefully, you can
see that the number of tetrahedral edges that come together in each
edge of the cubical lattice is actually 6, and so the net resistance
per cubical cell ends up as1, as required. (We assume unit cubes with
unit specific conductance here)
The resistor values of the left chopped up cube are 6 for the straight
edges, and 12 for the diagonal ones. Check that again, the resistance
across a unit cube of a cubical lattice is equal to 1.
So in 3D there are more ways of chopping things up, but the
dissipation and currents remain correct.
For triangles with the properly chosen resistor values, the net current
at a vertex is always half the continuous flux across the opposite
side. This means that the total current through a discretized slice is
invariant under deformations of the discretization, provided we change
the resistor values in accordance. This too, works in any dimension:
the net current at a vertex on an N-simplex
with properly chosen
resistors is 1/N!
times the
continuous flux through the corresponding
(N-1)
simplex opposite the
vertex.
But there is an easier way to see that any assembly created by
"clicking together" triangles using our method will have the correct
impedance across a slice of discretized space. This is because we know
that not only the voltage gradient is the same for the discrete and the
continuous case, but also the dissipation. This can only be true if the
total current through the region is the same.
Circuit equivalents of higher order discretization of continua
In most of this article we look at circuits in which only vertices that
are
neighbours (in the space they are embedded in) are connected by edges.
It
seems natural to ask: "What about circuits that involve
neighbours-of-neighbours?"
 Interestingly,
these can be used
to represent higher order
approximations
of continua. Below is a circuit that connects neighbours and
(neighbours)2.
Interestingly,
these can be used
to represent higher order
approximations
of continua. Below is a circuit that connects neighbours and
(neighbours)2.
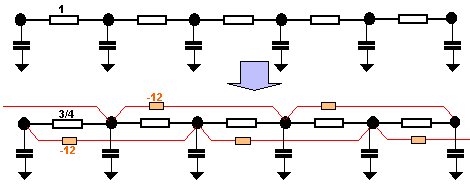
Circuit
for a second order
approximation of 1 dimensional time
dependent heat conduction.
The question is: Which values should be chosen for the resistors?
For each point, the equation for static equilibrium in terms of
temperatures (T)
is:
It is simply that each T
is a weighted average,
with the weight factors
equal to the the reciprocals of the connecting resistors. Comparing
this
to a second order approximation of the Laplacian, which can
be found
by inserting a Taylor series expansion into expressions for the
temperature
at points T(x0),
T(x0+Δx),
T(x0+2Δx),
T(x0-Δx),
T(x0-2Δx),
we find that:
R_neighbour = 3Δs2
/(4 λ
ΔVolume)
R_neighbour_neighbour = -12Δs2
/( λ
ΔVolume)
The extra resistors are negative!
Higher order circuits work in higher dimensions and in other analogies
too. But they are a bit tedious to explicitly construct for each case.
Higher order circuits can be computationally more efficient than first
order ones, especially if an accurate approximation of a
continuous system is needed. The burden of the extra resistors is more
than compensated by
the fact that a coarser discretisation still gives accurate results.
But
the interpretation of the network becomes trickier.
Higher
order differential equations
In the previous paragraph, we used neighbours-of-neighbours
connections, and tuned the R-values to eliminate the higher
derivatives. But we could have also tuned them to eliminate the second
derivative,
for example to create an equivalent for the bending beam equation.
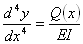

(
Wikipedia
image)
Cut
functions
An important concept, which is not often discussed elsewhere, is what I
call a "cut function".
A cut function on a vertex-edge pair is simply the voltage on the
vertex times the current through the edge. They should not be confused
with the power located on an edge. The latter are N-chunks,
located
on edges. Cut functions are (N-1)-chunks,
located on vertex-edge pairs,
that measure power flowing from one part of a circuit to another.
Suppose you "cut" a circuit in two, as shown
below. The currents are assumed to continue running, so the "cut" is
just an imaginary partition. It turns out that the power that flows
into a subcircuit is equal to the cut function of the edge that was
"cut off".
From Kirchhoff's current law, it follows that the sum of the cut
functions on a vertex is zero: No net power flows out of a vertex, as
is required for the conservation of Power.
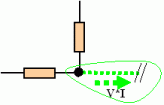
This is how it works out for a single resistor:

The resistor dissipates I(V1-V2).
On the left, a power I V1
flows in. On
the right a power I
V2
flows out (less than what goes in!). The
difference of incoming power and outgoing power is equal to what is
dissipated.
Cut functions work for non-dissipative circuits too: On the left, the
quantity I
V
is the power flowing out of the capacitor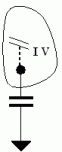 It
equals the rate of decrease of capacitive energy.
It
equals the rate of decrease of capacitive energy.
The difference between resistor dissipation and cut functions is that
cut functions represent flows in and out of regions, (N-1)-chunks.
They are not located on edges, but on edge-vertex pairs. In the case of
the Maxwell
circuit, the cut
function corresponds to the Poyting vector.
Now that we know the power that flow in and out of circuits, we can
immediately understand Tellegen's
theorem:
The total power in an isolated circuit is zero. (We know this
from
experience; you always need a battery. But the theorem applies to very
general situations)
Acoustic
fields
Acoustic fields works like
heat conduction, but now the
resistors are replaced by induction coils. Acoustic fields are
reversible, they have no resistors. The requirement that the total
dissipation is zero no longer requires that there is a source of energy
to have non-zero solutions, because the argument depended on the
resistances being always positive; they are now imaginary.
These sourceless non-zero solutions are of course: waves!
Set up the analogy
:
V
(Voltage) <-> p
(Pressure)
I
(Current) <-> vΔA
(Volume flux)
P
(Electrical power) <-> P
(Acoustic power)
C
(Capacitance) <-> ΔVolume/(κp0)
(Acoustic impedance of a volume)
L (Inductance) <->
ρ(Δs2)
/ΔVolume
(Acoustic impedance of an incompressible duct)
Figure
2: Electric circuit
equivalent for acoustic fields.
Applying Kirchhoff's
current law , and dividing
by Ci:
dp/dt
= -κp0/ρdiv(ρv)  dpi/dt
= -1/Ci
∑j(vΔA)ij
dpi/dt
= -1/Ci
∑j(vΔA)ij
Applying Ohm's
law across an inductor:
d(ρv)/dt
= - grad(p)  d(vΔA)ij/dt
= -(pi-pj)/Lij
d(vΔA)ij/dt
= -(pi-pj)/Lij
Combining:
d
2p/d
t2
=
κp0/ρ ∇2p
d
2pi/d
t2
= 1/
Ci
∑
j(
pi-pj)
/Lij
On the left sideof the above
equation is the acoustic wave
equation, with c2
= κp0/ρ.
The right side
is its discrete counterpart.
As an interlude to all the equations, an
animated GIF of an acoustic circuit in one of its eigenmodes:
Animated
GIF of acoustic
circuit. The magnitude of the
velocity is animated
as change in inductor width, the magnitude of the pressure is animated
as
the size of the bars attached to the capacitors.
Generating functional
:
S = d/dt
∑edges
( ½mv2
) + d/dt
∑vertices
(
½Cp2
)
= d/dt
(total energy
stored in components)
To retrieve the field equations
from this generating
functional, it is probably nicel to use space
time diagrams,
in which
the the principle of minimum dissipation is replaced by the principle
of least Action.
The
Navier-Stokes equation
The acoustic equations can be
modified to also include terms
to account for the transport or advection
of inertia, and for viscosity.
This leads to the Navier Stokes
equation,
which describes fluid dynamics. Fluid dynamics is non-linear, and has
funky
features like pseudo unpredictability.
The central idea for
transforming the linear circuit theory to
the non-linear stuff like Navier Stokes, is what I call a bucket
The idea is shown
below.
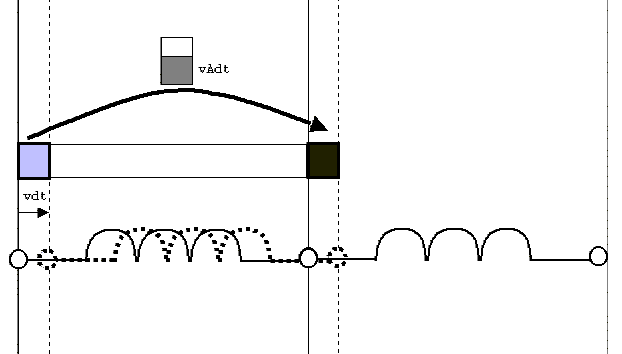
Figure
3: Principle of bucket discretisation of
advection.
After each time step, the fluid will be displaced relative to our cell
structure.
So we have to redivide the fluid among the cells each time step. We do
this
by interchanging buckets. It can be seen from the drawing that the
interchanged
bucket size is vA
dt.
The
buckets carry with them all information of the fluid, i.e.
all dynamical variables such as v,
p,
T,
etc.
It is possible to view this process as a coordinate transformation from
material coordinates,
which are attached to the
fluid, to spatial coordinates,
which are fixed in
space.
Suppose at time t,
we had a cell (i),
which has buckets leaving to a set of neighbours (j)
with volume velocities vij
Aij,
and had incoming buckets from a
set of cells (k)
with volume velocities vki
Aki
. By bookkeeping an arbitrary
dynamic variable (φ)
in the cell, we get:
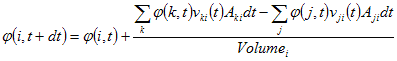
Which is the discrete version
of the advection term in fluid
dynamics:
dφ/dt
= -(v.∇)φ
+ ...
The central non-linearity comes
from the fact that v
itself
is also advected:
dv/dt
= -(v.∇)v
+ ...
A good thing about the buckets is that it automatically takes care of
some
nasty subtleties regarding discretisation schemes which can easily
cause
numerical instability. (For example, the direction of the flow
influences
the way we treat a neighbour) The simulation
software
I made using the
bucket
idea turned out to be very robust.
We will symbolize the advection
by a bucket drawn at each edge. We then get a diagram for the
compressible
Navier Stokes equation.
Figure
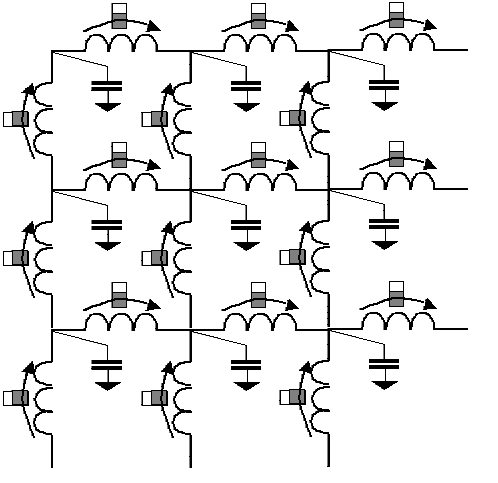
4: Electric circuit
equivalent of the Navier Stokes
equation for compressible fluid dynamics.
The Navier Stokes equation can
be further refined by including
viscosity.
Here is a cool picture of a Von
Karman Vortex street,
made
with a simulation
based on the modified acoustic equivalent.

Figure
5: Simulation result of Navier Stokes: A Von
Karman vortex street
Navier
stokes on an
arbitrary trianglular net
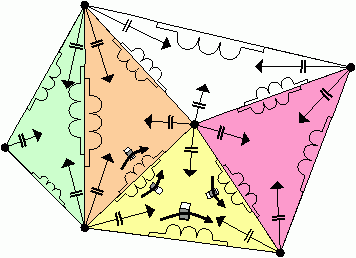
When we try to implement the
Navier Stokes equaiton on an
arbitrary
triangular network, we encounter an additional difficulty. We
can use the previously found methods to find all the impedances, and
use the bucket formula to transport properties from vertex to vertex.
But what is the momentum that we should assign to a vertex?
I have just about finnished writing an article on this, in which I
think I figured out how to do it.
The
Klein Gordon Equation
An interesting network is that
below, which turns out to be an
equivalent of the Klein Gordon equation.
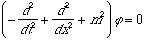
The Klein Gordon equation is
the relativistic wave equation
for spin zero particles. The network is drawn for one dimension (x),
and with two layers, UP an DOWN. We derive:
Figure
6: Electric circuit
equivalent of the Klein Gordon
equation, with 2 possible modes.
The equation splits into two superposed modes, the symmetric ( UP+DOWN)
and
(UP-DOWN). The two modes both obey the Klein Gordon Equation. The
symmetric
mode has mass zero, and the anti symmetric mode has mass (Ly
C)-1/2
. Jos Bergervoet has suggested
a simpler circuit for the Klein Gordon Equation:
Figure
7: Electric circuit
equivalent of the Klein Gordon
equation, with 1 possible mode.
The equation for this circuit
is:
It only has one mode (particle
species) as opposed to the previous
circuit, which had 2 modes.
Electrostatic
fields
Set up the analogy
:
V
<-> V;
ΔxV
(Voltage
difference in x-direction) <-> -
Ex
Δx
(Chunk of Electric field)
Q
(charge) <-> Q
(charge)
I (current) <-> d(DΔA)/dt
(rate of change of dielectric displacement through surface)
Cx
(Capacitance placed in x-direction)
<-> ε
ΔVolume/Δx2
(Storage container of Electrostatic field energy)
Figure
8: Electric circuit
equivalent for electrostatic fields
Kirchhoff's current law:
d/dt
(div(D))
= 0  0 = ∑j(d/dt
(DΔA))ij
0 = ∑j(d/dt
(DΔA))ij
Ohm's law:
D = -grad(V)/ε (DΔA)ij
= -1/Cij
(EΔs)ij
= -1/Cij
∑ij(Vi-Vj)
(DΔA)ij
= -1/Cij
(EΔs)ij
= -1/Cij
∑ij(Vi-Vj)
Combined, this gives:
d/dt
(∇2V/ε
) = 0  d/dt(-1/Cij
∑ij(Vi-Vj))
= 0
d/dt(-1/Cij
∑ij(Vi-Vj))
= 0
Usually, you say that at t=0,
the
divergence of the field is equal to the charge density. You then get:
∇2V
= ρ/ε
Kirchhoff's voltage law gives:
d/dt
(curl(E))
= 0
The Generating functional
is:
S = d/dt
∑(E.D ΔVolume)
E.D is the
field energy density.
To retrieve the field equations
from the generating
functional, we have to write it in terms of Vi:
S = d/dt
∑ij (
½Cij
(Vi-Vj)2
)
Comment
on E
versus D
It can sometimes seem a bit irritating to have 2 different quantities
associated with electric fields (E
and D
). In principle, this can be avoided, just like it can be avoided to
use
currents by always writing them as a voltage difference divided by a
resistance.
But I think it is important to distinguish between 1-chunks like Ex
Δx
and (N-1)-chunks
like Dx
ΔVolume/Δx
. This distinction is analogous to the distinction between electric
potential
and electric current, a distinction that we would surely want to be
aware
of when we repair household electra.
Comment
on field energy
This representation may seem somewhat artificial, the vacuum is
supposed
to be empty, and not contain any capacitors. However, the vacuum does
contain
electrostatic energy, which is stored locally in the vacuum. This
energy
is the same energy that is stored in the imaginary capacitors. So they
are
not that abstract as it seems: the energy is really there.
Putting
in conductors
You just put resistors in parallel to the capacitors. Interestingly,
short-circuiting
capacitors increases the capacitance of a geometry, thereby also also
decreasing
the effective speed of light through the geometry. This can be seen
easiest
in one dimension. Suppose a number of capacitors are connected in a
chain.
From Kirchhoff's
voltage law it follows that when
impedances are in series,
you get the effective impedance
of the chain by adding the individual impedances. This means that the
for
the effective capacitance (Ceff): 1/ Ceff = 1/C1 + 1/C2 + 1/C3 + ... If
we
short-circuit some capacitors in the chain, the reciprocal of the
effective
capacitance gets smaller, so the effective capacitance itself gets
bigger.
The
Maxwell equations
The Maxwell equations describe both electric and magnetic phenomena,
and
their interaction. So this is stuff that you need to understand if you
want
to understand nature. To put Maxwell into a circuit diagram, you start
with
the diagram for electrostatic
fields . Then, we have to think
how we can put in the
magnetic field. We think
naturally of inductors, as they seem to be the magnetic counterparts of
capacitors.
But it is a bit tricky. We know that the vacuum does not conduct
electricity,
so we can't put any inductors in parallel with the capacitors. We could
try
putting them in series. But that would mean that there is only magnetic
energy
when a current is flowing through the inductors, and therefor also
through
the capacitors. But this would charge them up indefinitely, and produce
infinite
electrostatic fields. The clue comes from the observation that an
inductor
is not 'elementary', when you look at its geometry. It consists of a
coil,
a spiral of wire. The elementary object is a single loop. After a
considerable
struggle with this idea, I realized that a proper treatment requires a
new
concept, the
mesh inductance. This is an
inductance associated with a loop
rather than an edge.
Generalizing
a circuit to an N-complex
This idea is part of a cool generalization of a circuit,
called a N-complex, or
cell complex. A
conventional circuit can be thought of as a 1-complex. The idea will be
brought along from the following list:
0- Complex : a set of loose
Vertices (points) or 0-chunks
1- Complex: (=Concentional circuit): Edges (or 1-chunks) that connect
Vertices
2- Complex: Faces or 2-chunks that connect Edges
3-Complex: Solids or 3-chunks that connect Faces
N-Complex:
N_chunks
that connect
(N-1)
chuncks
So how do we generalize
Kirchhoff's laws and Ohms law? We
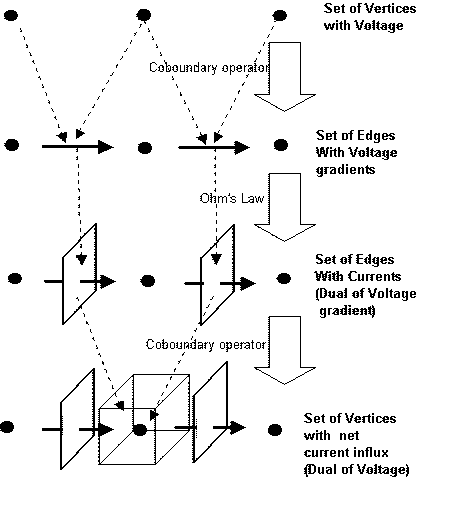
first need the concepts boundary
and the coboundary
operators.
Boundary and co-boundary operators are just mathematical formalizations
of
what we intuitively understand right away from the diagrams. Roughly,
the
boundary of an n
-cell is the set of [n-1]
cells that form
its boundary. The (co)boundary operator will also take care of some
minus
signs book keeping, associated with the orientation choices of the
positive
directions.
Suppose we have N
vertices and M
edges. Then the Boundary
operator for Edges can be thought of
as an ( N
X M)
matrix({
aij}),
that has entry aij=0
if the vertex (i)
is not connected to the edge (j),
aij
= -1 if it is the source of the
chosen arrow on the edge, and
aij
= +1 if it is the destination of the chosen arrow on the edge. The
arrows
can be chosen arbitrarily, but once chosen, we should of course keep
them
fixed.
The coboundary of the set of k-chunks
gives the set
of k
+1 chunks that has the k-chunk
as a part of its boundary, once
again taking care of all minus
signs
and arrow orientations etc. The Coboundary matrix for the Vertices is
simply
the transpose of the Boundary matrix for the Edges.
Reformulating
a conventional circuit (1-complex) into
our new jargon
Now we are armed to formulate ordinary circuits in a new jargon, which
will be useful when we start to generalize further.
Step 0. We define a
voltage (Vi)
on each Vertex.
Step 1. We let the Coboundary
operator act on the Vertices (as
the discrete analog of the differential Grad
operator)
producing a set of 1-chunks:
Coboundary (Vi)
= ΔVij
(Step 1)
This is familiar, we just take
the voltage difference across
each edge.
Step 2. We apply
Ohm's law to to map our 1-chunks to
twisted N-1
Chunks:
Iij
= ΔVij/Rij
(Step 2, or Ohms law)
In 3 dimensions, a chunk of current will scale with area. In N
dimensions, this generalizes to a N-1
dimensional
subspace. Such a subspace will generally have an arrow associated with
it.
In the case of a surface, we think of the normal vector of the
surface.
So why is the chunk called
"twisted"? This is because its arrow direction
is always inherited from the voltage difference, rather than from its
own
geometry. Another way to see this is that the spatial information
contained
in the resistance value
Rij
is stripped of its arrow; it is always positive. So
Iij
always has the same arrow as ΔVij.
And, if you take the product Iij
ΔVij
you get an N-chunk
of generating functional, which has an always-positve volume associated
with it, in contrast to an oriented volume that non-twisted chunks
would
produce. When we study the Dirac equation, we will put step 2 and 3
together to form the twisted
coboundary
.
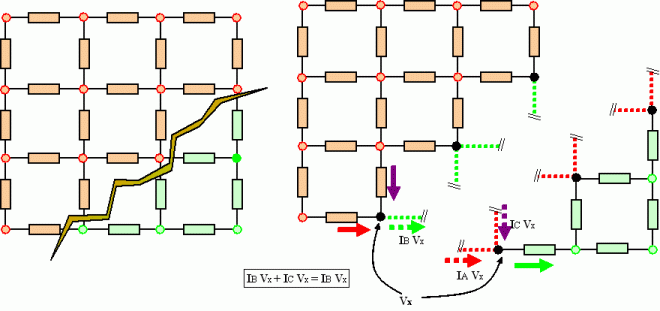
Step 3: Generalize Kirchhoff's
current law.
Coboundary(Iij)
= 0 (Step3, or the generalized
Kirchhoff's current law)
It may seem a bit strange at first that we use the coboundary rather
than
the boundary. After all, vertices are the boundary of edges. But in
step
2 we made currents N-1
chunks, and the coboundary
of N-1
chunks should be a set of N
chunks. These N
chunks are just the dual of the
0-chunks on the vertices. See figure 9 for an illustration.
Once again, there is an analog
differential operator, this
time the div operator.
Kirchhoff's current law is
always about incoming fluxes that have to add up to zero.
Figure
9: Structure of the laws
of electric circuits in terms
of coboundaries.
Combining Step 1,2 and 3, we
find the set complete of
equations for a 1-complex:
Coboundary(Ohm(Coboundary(Vertices)))=0
What about Kirchhoffs voltage law? We already have a complete
mathematical
description of the circuit, so the voltage law can be viewed as an
alternative
formulation. It reads:
Coboundary (ΔVij)
= 0
or combining with a previous
formula:.
Coboundary (Coboundary (Vi))
= 0
This can be derived directly
from the general theorem that the
Coboundary of a Coboundary is
zero. (Also the Boundary
of a Boundary is zero ). These 2
statements are important
fundamental laws. They can be visualized
if you play around a bit with circuits and arrows, perhaps writing out
the
boundary matrix.
Note:
The div,
curl and
grad operators
are all instances of Cartan's
exterior derivative (d).
Thus, the
Coboundary operator is the discrete analog of Cartan's exterior
derivative. Ohm's law is the discrete analog of the Hodge
star
operator , multiplied by a
material constant.
Formulating
the Maxwell circuit as a 2-complex
For Maxwell the electric field on an edge can no longer always be
expressed
as a gradient of a potential. This is typical of a 2-complex. So we do
not
start by defining a potential of vertices, but 1 dimension
higher:
on the Edges. This is the diagram:
Figure
11: Electric circuit
equivalent of the Maxwell equations
With the analogy
:
V
<-> V
(Voltage)
ΔxV
<-> ExΔx
(Chunk of Electric field)
Q
<-> Q
(charge)
Jz
(Mesh current)
<-> HzΔz
(Chunk of Magnetic field)
Cx
<-> ε
ΔVolume
/Δx2
(Storage container of Electrical field energy)
Lz
<->μ
Δz2
/ΔVolume
(Storage container of Magnetic
field energy)
Step 0: Each edge has a 1-chunk
EΔs
associate with it, that we call an E-chunk.
Step 1: Take the coboundary of
the set of E-chunks.
This will give you a set of loops. Note also that there are many
different loops that we might want to choose, that all traverse the
circuit.
We could even in principle choose loops that go round a track 10 times.
But the
only physically relevant loops are those that we give a finite mesh
impedance.
In our Maxwell diagram, only the loops that are inside the faces of the
cubes
have finite impedance and are used. It will be convenient for later to
ignore loops that will not get a finite impedance.
Anyway, after taking the
coboundary of the E-chunks, we will
have performed the discrete analog of curl(E).
curl(E)
= -d/dt
B  ∑along_loop
EΔs
= -d/dt(BΔA)
∑along_loop
EΔs
= -d/dt(BΔA)
We will use this as a
definition of B,
or
magnetic induction. The d(BΔA)/dt
are 2-chunks, that we will call B-chunks.
Step
2: Apply Ohms law, but now use
the
mesh inductance to map the B-chunks which are 2-chunks
onto twisted
N-2 chunks, which we
define as H.
In 3
dimensions, H
comes in twisted 1-chunks of HΔs,
or vectors associated with a loop. The vector
will be recognized as the normal vector of the loop. The equation is
the
discrete analog of:
H
= (1/μ)
B  BΔA
= 1/Lmesh(HΔs)
BΔA
= 1/Lmesh(HΔs)
Step
3. Take the Coboundary of the H-chunks.
curl(H)
= dD/dt ∑along_loop
HΔs
= d/dt(DΔA)
∑along_loop
HΔs
= d/dt(DΔA)
Step
4. Once more apply Ohms law, but
now
over the capacitances at each edge, we get the discrete analog of:
E
= (1/ε)
D EΔs
= 1/C(DΔA)
EΔs
= 1/C(DΔA)
Summarizing, we have the
Maxwell equations:
curl
(E)
= -dB/dt
H
= (1/μ)
B
curl(H)
= dD/dt
E
= (1/ε)
D
Application of the generalized
Kirchhoffs Voltage law by
taking the coboundary of the coboundary of E
and H
:
d/dt
(div(D))
= 0
d/dt
(div(B))
= 0
It is generally axiomized that
at t=0,
we
have:
div
D =
ρ
div
B = 0
Note that we can have magnetic energy without having to charge the
capacitors.
For example, a constant magnetic field would correspond to identical
mesh
current in each loop. This means that the net edge currents are zero,
so
the capacitors are not being charged. The magnetic energy is stored
inside
the mesh inductance. Once again, this energy is real in the sense that
it
is locally present in the vacuum.
The Maxwell equations can be
combined to form the
electromagnetic wave equation:
The model presented for the
Maxwell equations could be seen
as an aether
model . In
the link, it is argued that this does not violate relativity.
Putting
in conductors
This is the same as with electrostatic fields, you just put resistors
in parallel to the capacitors.
Putting
in compact components
Sometimes components much smaller than a wavelength can influence the
field.
This is especially the case with resonators. They can resonate at a
frequency
much lower than the frequency that is associated with c/s . (s is a
typical
dimension of the system) To put in these components, you just add them
to
the circuit. You don't have to create the whole geometry, you can just
put
a big physical capacitance across a small 'vacuum' capacitor, which
will
then become negligible. Likewise you can put in coils, not a spiraled
conductors
but as single circuit elements. Then you can start to calculate how
this
physical circuit would interact with the vacuum.
Visualizing the
dynamics:
To visualize an electromagnetic wave, you can picture a line of
capacitors
being charged at time=0. Along this line you would have a constant
E-field,
pointing along the line. This causes a voltage difference across
neighbouring
parallel lines of capacitors. This causes a current to flow,
discharging
the first line of capacitors, and charging the neighbouring ones. But
this
current corresponds to mesh currents. So as the neighbouring E-field is
being
built up, some of the energy is being transferred to magnetic energy in
the
meshes. By the time that the fields of the neighbouring lines are equal
to
the field of the original line, there is no capacitive driving force to
displace
more charge. But now there is inductive driving force, which acts like
an
inertia. The transport of charge continues, now against the direction
of
E. This is similar to a mass/spring system, where the mass will move
against
the force of the spring, once it has gained momentum.
In the meanwhile
capacitive energy is being transferred to neighbours-of neighbours of
the
original line. So the energy spreads out into space. Unlike with heat
conduction, the process is reversible. The
energy is not dissipated, but is pumped back and forth from its
magnetic
form to its electric form.
Animated
GIF of a Maxwell circuit. The magnitude of
the magnetic field is animated as rate o
Below, an amimation is presented of a Maxwell circuit.
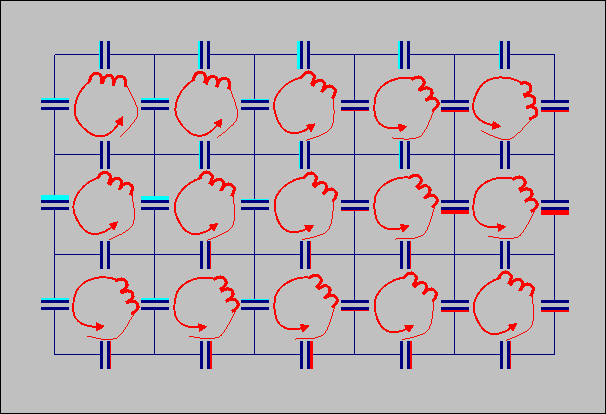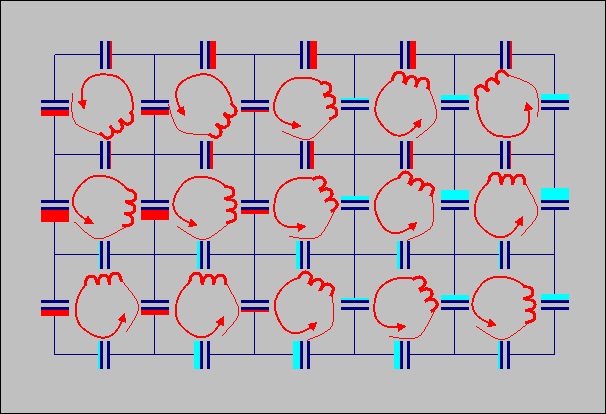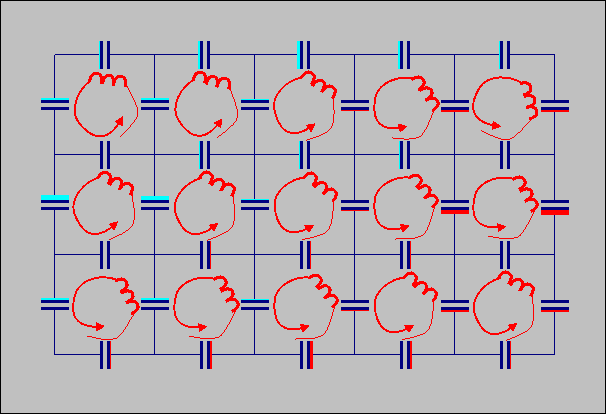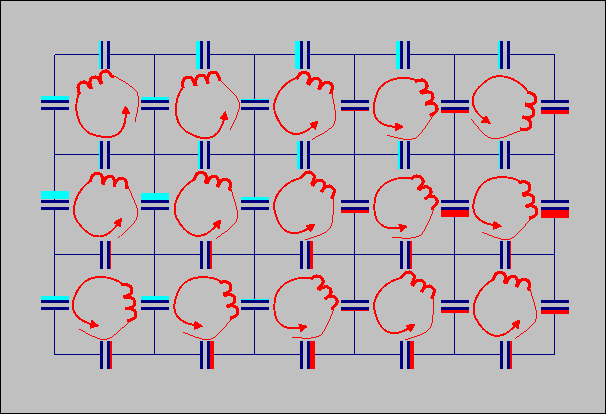
f
rotation
of the mesh inductors, the magnitude of electric field is animated as
the size of the colored bars attached to the capacitors.
The Poynting
vector of the
electromagnetic circuit is a Cut function:
It is assigned
to a edge-loop pair. We multiply the 1-chunk of E with
the (N-2)-chunk
of H
to get a (N-1)
chunk of power
flux (E
x H).
Note that the Poynting vector in 3D space is represented by more than 3
components in the circuit, which makes it seem unlike a vector. This is
because the Cut function becomes only a vector after being "contracted
with a cut": If you specify the cut (the analog of a surface), the cut
function gives you the flux across the cut at each point.
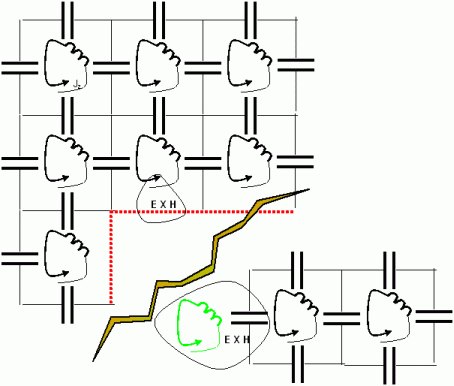
The
Poynting
vector as a cut function.
The Generating functional
for the Maxwell circuit is:
S = d/dt
∑edges (E.D
ΔVolume
)+ d/dt
∑ meshes
(H.B
ΔVolume)
= d/dt (
total energy stored in components)
To retrieve the field equations
from the generating
functional, we have to write it in terms E
only (A
form with H
instead of E is
also possible):
S
= d/dt
∑edges (½
Cedge
(EΔs)2
) +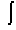 dt
∑meshes
(∑loopEΔs
)2
dt
∑meshes
(∑loopEΔs
)2
But this is more elegantly done
using space
time diagrams
, in which the the principle of minimum dissipation is replaced by the
principle of least Action.
The
Schrödinger equation
Another important equation in physics is the Schrodinger equation. (It
is
actually an approximation of the Klein Gordon equation.) It describes
the
quantum mechanical wave function of a particle in a potential field (
V ).
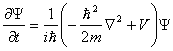
The Schrödinger equation looks almost the same as the heat conduction equation
. We need to
put in the potential V,
and to take care of i , the
square root of –1. To represent the potential (V),
we add resistors (r)
to ground potential.
The analogy
becomes:
V <->Ψ
1/r
<-> V
ΔVolume
1/Rx
<-> ħ2/(2m)
ΔVolume
/Δx2
C
<-> iħ
ΔVolume
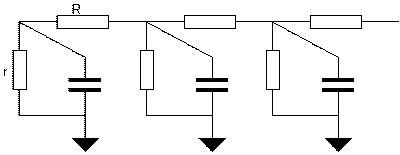
Figure 12: Electric circuit
equivalent of the Schrodinger
equation, with imaginary-valued capacitance.
These together yield the
Schrodinger equation, but we had to
choose an imaginary
capacitance. This is no problem mathematically, we can just do all
calculations
as we did with real numbers. But it is perhaps a concession to
visualizability.
A major consequence of choosing imaginary capacitance is that the
solutions
are now of the type:
Ψ
~ exp(ikx)
exp(-iωt)
rather than
Ψ
~
exp(ikx)
exp(-t/τ)
A subtle but important difference: It means we don’t get
exponential decay
with time into thermal equilibrium as with heat conduction but we get
everlasting
oscillations which conserve |Ψ|2.
Another approach is to try to
write out
Ψ into real
numbers Ψ
= ( X
+ iY
). We then obtain
equations for X
and Y
that are
of the form:
d2X
/dt2
= d4X
/dx4
This equation is like the equation for waves in a bending beam. You can
make
a kind of beam construction using springs and bars. This has led to a
mechanical
discrete analog of the Schrodinger equation with springs and rods, that
sometimes
pops up in literature. I don't know if it can be built using electrical
components.
Space-time circuits
So far, we have considered discrete space, but time has till now been
considered
continuous. Interestingly, it is possible to construct a model that has
space
and time discretized in the same way. I like this, because according to
the
theory of relativity, space and time should be deeply related.
The trick is to put negative
resistance in
the time direction.  This sign
is related to the negative sign of the
time component of the metric of space-time.
This sign
is related to the negative sign of the
time component of the metric of space-time.
As an example, we will create
the acoustic wave equation in
terms of a space-time circuit.
We will use the so-called Velocity potential as the analogue
of
Voltage.
Set up the analogy
:
V (Voltage)
<-> φ
(Velocity potential)
Ix
(Electric current in x-direction)
<->(ρvΔAΔt)x
(Mass displacement in x-direction)
It
(Electric current in t-direction)
<-> p
(ρ/(κp0))
ΔVolume
(Pressure times spatial volume)
P (Electrical
dissipation) <-> S
(action)
1/Rx
(Electrical conductivity
in x-direction)
<-> ρΔVolume
Δt
/Δx2
1/Rt
(Electrical conductivity
in t-direction)
<-> -(ρ/(κp0))
ρΔVolume
Δt
/Δt2
Note that (ρ/(κp0))
= c2,
the speed of sound squared.
Draw the following circuit :
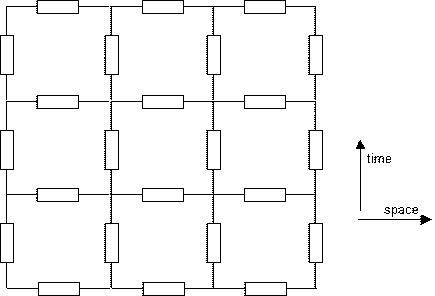
Figure
14: Electric circuit equivalent of the scalar
wave equation discretized in both space and time.
The velocity potential (φ)
is
defined such that:
v
= -grad φ
p/ρ
= -dφ/dt
Velocity and pressure
live in
the circuit as voltage
differences across edges (i.e. as 1-chunks):
vxΔx
= -Δxφ
p/ρΔt
=
-Δtφ
Write out Kirchhoff's current
law at a vertex (using Ohm's law
to get the currents):
(ρvΔAΔt)x[x,t]
- (ρvΔAΔt)x[x-Δx,t]
+ (ρ/(κp0))p[x,t]
ΔVolume -
(ρ/(κp0))p[x,t-Δt]
ΔVolume
= 0
Divide by ρΔVolumeΔt
(assumed constant for the moment) and rearrange:
(
p[x,t]
- p[x-Δx,t]
)/Δt
= - (1/(κp0))
( vx[x,t]
-
vx[x,t-Δt]
)/Δx
Which is the discrete analog of:
dp/dt
= -(1/(κp0))
div
v
Next, write out Kirchhoff's
voltage law around a loop:
vx[x,t]Δx
+ p/ρ[x+Δx,t]Δt
- vx[x,t+Δt]Δx
- p/ρ[x,t]Δt
= 0
This time, divide by Δx*Δt/ρ,
and rearrange:
(
ρvx[x,t+Δt]
- ρvx[x,t]
)/Δt
= -( p[x+Δx,t]
- p[x,t])/Δx
Which is the discrete analog of:
dρv/dt
= -grad p
So we once more have the acoustic wave equation, but now
in space-time form.
There is now no longer a role
for the inductors and
capacitors, the only component is the resistor.
The Generating functional
is now
S
= ∑edges ΔV2
/R
=∑x-edges
(ρvx2)
ΔVolume Δt
- ∑
t -edges
(p2/(κp0))
ΔVolume Δt
=∑edges
(dφ
/dxμ)(dφ
/dxμ)
ΔVolume Δt
The generating functional is
now Action  instead
of dissipation. The "dissipation" in this analogue has of course no
longer anything to do with energy loss.
instead
of dissipation. The "dissipation" in this analogue has of course no
longer anything to do with energy loss.
Action is a fundamental quantity, perhaps even more fundamental than
energy.
In a sense, it is energy density integrated over space and
time.
According to quantum mechanics, there is a fundamental chunk of action,
equal to ħ.
More on that in the future.
Note that the use of negative
resistances in the time
direction means
that the total action (<->dissipation) in the circuit is
zero.
We can also put the Klein
Gordon equation in space-time form,
by connecting
a resistance to ground potential to each vertex. The mass term is
represented
by a current to ground.
Application:
The discrete time harmonic oscillator
We can use the idea
of space time circuits to make a discrete
time harmonic oscillator, a zero dimensional wave
equation.
The harmonic oscillator, with dynamic variables (x,p)
can be represented by a continuous-time
circuit equivalent:
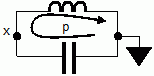
The position (x)
corresponds
to voltage, the momentum (p)
to current.
In discretized time, both position and momentum become
currents.
We get a ladder-like network, one resistor wide for the 'space
direction', and again, the resistors in the time direction are
negative. In the example below, we worked out a case with the time
resistors equal to -0.6 times the space resistors.
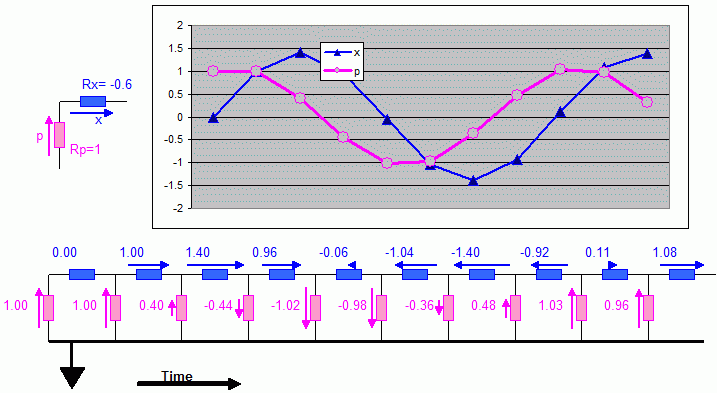
We can write down dynamic
equations to get from time (t)
to time (t+1):
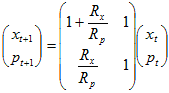
The system has an exact
solution:
I believed for a while that
space time circuits do not have
solutions
that conserve energy in the time direction, but I was pleased to find
that actually  they do: The eigenvalues of
the dynamic
equations are complex conjugates with unit magnitude, as long
as
they do: The eigenvalues of
the dynamic
equations are complex conjugates with unit magnitude, as long
as 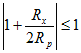 .
(Remember Rx is negative)
.
(Remember Rx is negative)
The dissipation in the resistors represents chunks of Action:
Energy times
time-interval.
Space-time circuit for the Maxwell equations
In the diagram below, we apply
the idea of a space-time
circuit to the
Maxwell equations. It all works out nicely, and  we obtain the
relativistic
formulation of the Maxwell equations in terms of the 4-vector potental (A)
and field tensor (F).
we obtain the
relativistic
formulation of the Maxwell equations in terms of the 4-vector potental (A)
and field tensor (F).
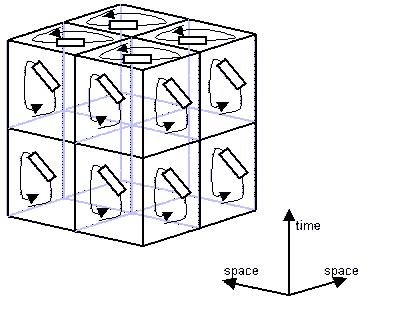
Figure
15: Electric circuit equivalent of the Maxwell
equation discretized
in both space and time. To depict it in 3D, we draw only 2 dimensions
of
space.
The capacitors and mesh
inductors are replaced by mesh
resistances. Like
in the scalar case, the dissipation in these resistors is reinterpreted
as
Action. Again following the scalar case, the mesh resistances which
have a time component (Rtx,
Rty,
Rtz)
are negative, so that
the total action in the circuit is zero even with non-zero currents.
We do not use a scalar potential φ,
but
a vector potential A,
a 1-chunk of which (AμΔrμ)
is defined on each edge. In (3+1) space-time dimensions, there are 4
components of A
, and 3+3 components F.
The 3+3 components
of the electric
field and the magnetic field are now contained in the 6 mesh F-chunks FμνΔrμΔrν.
Lets remind ourselves of the
relation between F
and A,
and their more familiar friends E
and B:
Fxy
= dAx/dy
- dAy/dx
= Bz
Fzx
= dAz/dx
- dAx/dz
= By
Fyz
= dAy/dz
- dAz/dy
= Bx
Fxt
= dAx/dt
- dAt/dx
= Ex
Fyt
= dAy/dt
-
dAt/dy
= Ey
Fzt
= dAz/dt
- dAt/dz
= Ez
or, using 4-index notation:
Fμν
=
dAμ/drν
-
dAν/drμ
 FμνΔrμΔrν
= (dAμ/drν
- dAν/drμ)ΔrμΔrν
FμνΔrμΔrν
= (dAμ/drν
- dAν/drμ)ΔrμΔrν
The mesh resistances Rμν:
Rμν
= εμν
(ΔrμΔrν)2
/ (ΔVolume Δt)
with
εμν
=
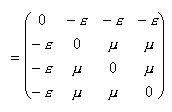
The Generating functional
is now the Action of the electromagnetic field:
S
= ∑meshes
(ΔμνA)2
/Rμν
Note the compactness of the
relativistic formulation of the
Maxwell equations.
If we impose Kirchhoffs current law on A, we get the discrete version
of the Lorentz gauge condition dμAμ
= 0.
Curved
Space time
With electric networks, you can
implement any
metric of space time. If dx,
dy,
dz
and dt
vary from place to place, as in curved space, you can just adapt the
impedance
values accordingly. Furthermore, there is a 1-to-1 correpondence
between the metric tensor in a simplexial chunk of space time and the
resistors on its edges, as we saw in the section on the N-simplex equation.
You could reinterpret the
changes values as being
caused
by a variable ε
and μ
constants of the vacuum. There are even people who tried to construct a
gravity theory on this principle, for example:
http://arxiv.org/abs/gr-qc/9909037
A link brought to my attention by Gordon D. Pusch.
Relation
of circuit analogies to bond graphs
Like
electric circuit analogies, Bond
graphs are a
way to model all kind of things in a unified way. The bond graph
aproach is more or less equivalent to the electric circuit analogy
approach. Below is a model of a 2D acoustic medium in both bond graphs
(red) and electric circuit (black). Bond graphs also use pairs of
variables whose product is power. The voltage-like quantities
are
called "effort", and they are located at nodes labeled "0". These nodes
also imply Kirchhoffs current law for the other, or "flow", variable.
The "flow" variables can be thought of being located at the "1" nodes,
on which Kirchhoff's voltage law is implied. The arrows are interpreted
as flows of power, or "Power bonds". The bonds go from "0" and "1"
nodes to element nodes. These elements force an equation between effort
and flow, just like circuit elements. Note that in the diagram below a
1-node is used to create a voltage difference, which is then coupled to
the inductance L.
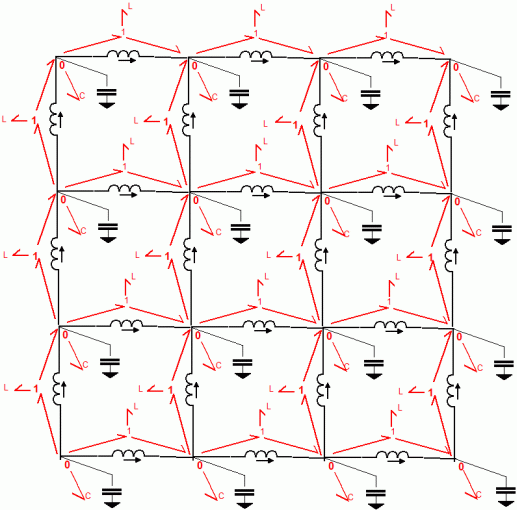
Bond
graph (in red) and circuit
equivalent (in black) of an 2D acoustic medium.
Bond graphs are often used in
models whith multiple domains, for
examplea loudspeaker, whic has an electric part and a mechanical part.
A similar transfer between elctrical and mechanical domains is possible
with electric circuit equivalents, using a transformer. A purely
electric transformer has a dimensionless winding ratio, but we can give
it a dimension, to convert from voltage/current to for example
velocity/force.
A
transformer can interface between
different physcal domains, eg from elctric to mechanical.
Some links
Eric Forgy has drawn my
attention to some links and literature
on related subjects. A good start is here:
http://math.unm.edu/~stanly/mimetic.html
I missed some of this literature previously, because different key
words
are used. For example I had never heard of Hodge star, co-boundaries,
etc.
(My excuse is that I am an engineer, normally working on very different
things)
A keyword is "mimetic" which means that a discrete system mimics a
continuum.
The keyword "cell method" refers to a discretisation method that is
much
like a circuit mathematically, but uses different symbolism. I have
tried
to learn the lessons from some of this literature, and incorporate it
into
this page.
Another place where I learned a
lot is this newsgroup:
sci.physics.reseach (Google
archives all messages)
And a new group, focussing on
discrete physics:
sci.physics.discrete (Google
archives all messages)
Further
work on electric circuits.
New results will be published when available. Specifically, I
am thinking of:
-interacting (non-linear) fields
-circuits with strange topologies (Mobius strip, Klein bottle, higher
dimensions)
-simulation
software
-quantum fields Any suggestions are welcome.
 A cool property of the total dissipation is that you can recover all
equations
for the circuit by requiring that the total dissipation is in a minimum
with
respect to small variations of
Vi
. Mathematically, this is saying all derivatives to Vi
are zero:
A cool property of the total dissipation is that you can recover all
equations
for the circuit by requiring that the total dissipation is in a minimum
with
respect to small variations of
Vi
. Mathematically, this is saying all derivatives to Vi
are zero:





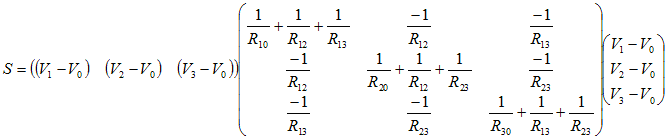
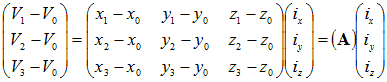

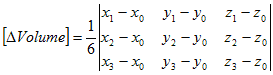
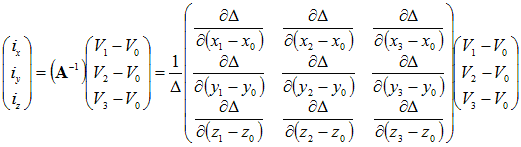
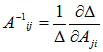
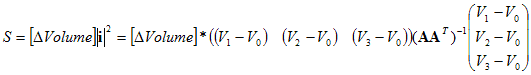
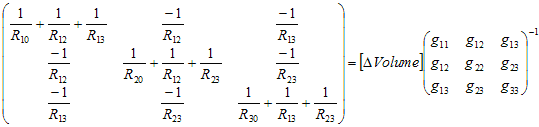
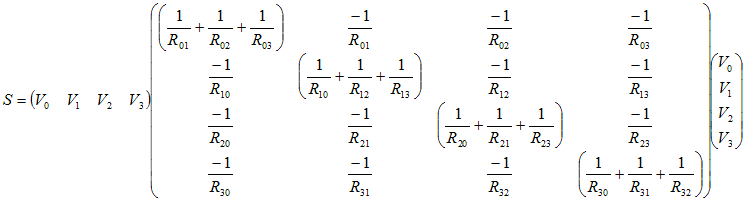
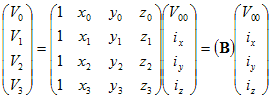
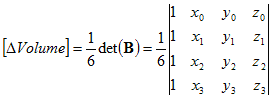
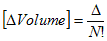
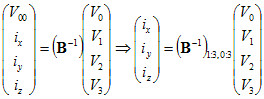
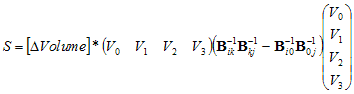
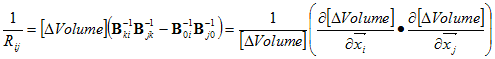
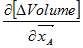 as
a pseudovector (A*)
whose direction is normal to the (N-1)
simplex built from all vertices except (A)
and whose magnitude |A*|
is
the (N-1)
volume, multiplied by a factor 1/N!.
as
a pseudovector (A*)
whose direction is normal to the (N-1)
simplex built from all vertices except (A)
and whose magnitude |A*|
is
the (N-1)
volume, multiplied by a factor 1/N!.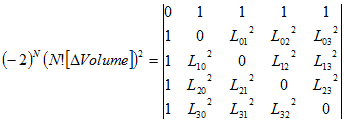
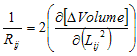

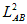 ,
while
keeping all other lengths constant. This means that the shape of the 2 (N-1)
simplices A*
and B*
cannot change,
and the motion of A and B will be parallel to our projection plane. We
split
the squared length (
,
while
keeping all other lengths constant. This means that the shape of the 2 (N-1)
simplices A*
and B*
cannot change,
and the motion of A and B will be parallel to our projection plane. We
split
the squared length (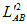 )
and a
component orthogonal to it (
)
and a
component orthogonal to it (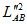 ):
):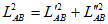
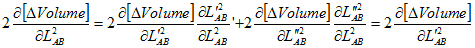
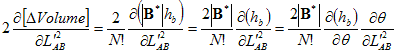
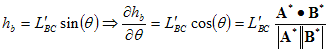
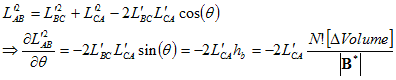
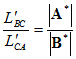 :
: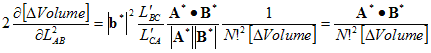
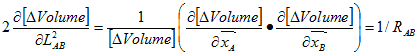
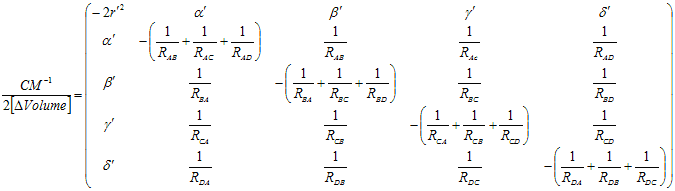

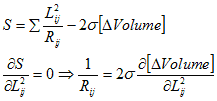

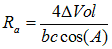
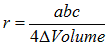
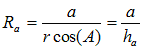



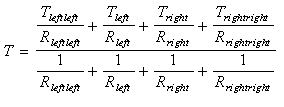
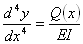


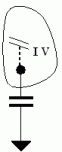 It
equals the rate of decrease of capacitive energy.
It
equals the rate of decrease of capacitive energy.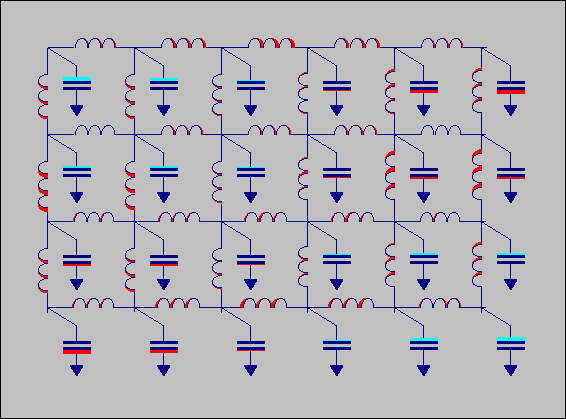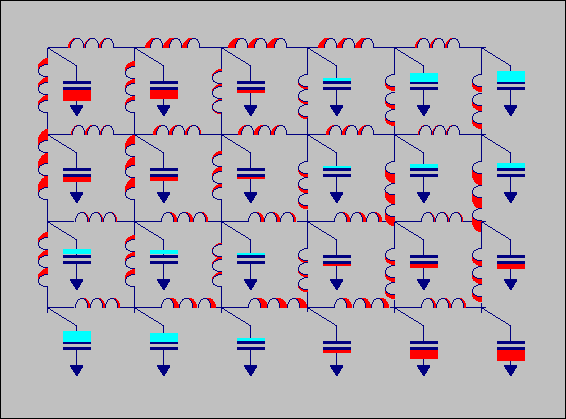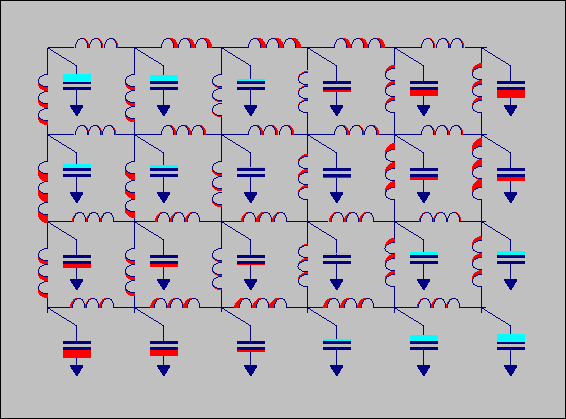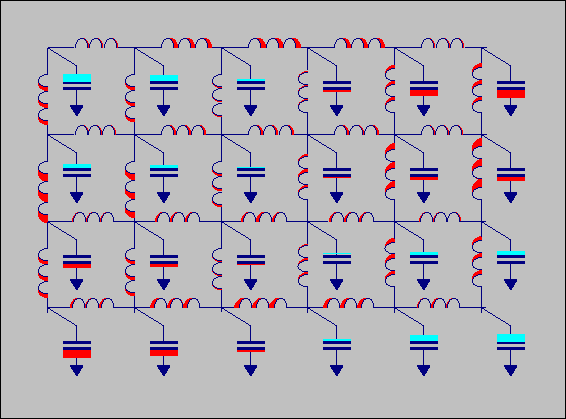

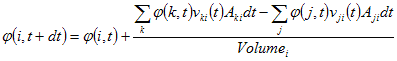



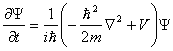


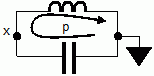

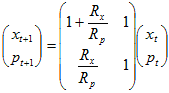
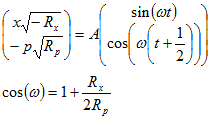
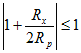 .
(Remember Rx is negative)
.
(Remember Rx is negative)